A Review of Bioinformatics Methods for RNA Secondary and Tertiary Structures Prediction

---

Author(s): Abdelhakim El Fatmi* and Molay Ali Bekri

Abstract

Initially, it was thought that Ribonucleic acid (RNA) primarily served as a carrier of information required for protein synthesis. However, recent discoveries have unveiled RNA’s pivotal involvement in gene regulatory networks and various cellular processes. The functionality of an RNA molecule is intricately linked to its structures, including secondary and tertiary (three-dimensional) structures. Consequently, comprehending the functions of RNA necessitates a thorough understanding of its diverse structural aspects.

Deciphering the secondary structure or tertiary structure of RNA from its primary sequence is a complex computational challenge. Consequently, several methods and techniques have been devised to address this issue. Initially, physical techniques like X-Ray, Crystallography, and Nuclear Magnetic Resonance were employed, but they proved to be expensive, labor-intensive, and time-consuming. As a result, the demand for bioinformatics methods has significantly increased to tackle this problem more efficiently.

In this paper, we will explore the various employed methods for predicting the different RNA structures, encompassing both secondary and tertiary structures.

Introduction

Ribonucleic acid (RNA) consists of a sequence of nucleotides: Adenine (A), Cytosine (C), Guanine (G), and Uracil (U). Within the cell, RNA molecules play crucial roles in diverse biological processes. While its initial well-known function involves transporting genetic information from DNA to proteins, it has been found to perform numerous other functions. Notably, the discovery of novel RNA classes, such as non-coding RNAs, like small nuclear RNAs (snRNAs), has expanded our understanding. These snRNAs combine with proteins to form small nuclear ribonucleoproteins (snRNPs) involved in RNA splicing. In general, an RNA molecule’s function is intricately tied to its structures, particularly its secondary and tertiary structures [1-5].

When seeking molecular structures, the final step involves predicting the three-dimensional shape of the molecule. Achieving high-precision predictions, especially for large RNA molecules with only their primary structure as information, remains a formidable challenge. Conventional physical techniques like X-Ray, Crystallography, and Nuclear Magnetic Resonance are not only expensive but also demand significant effort and time [6]. Consequently, RNA structure prediction has emerged as a vital area of interest for researchers and one of the foremost challenges in the field of bioinformatics.

RNA Structures

Primary, Secondary and Tertiary Structure

The RNA molecule exhibits a hierarchical organization with three structural levels: the primary structure, secondary structure, and tertiary structure [7]. The distinct functions of RNA are often revealed by analyzing its complex structures, particularly its secondary and tertiary structures [5] (see Figure 1).

Primary structure

The primary structure of Ribonucleic acid (RNA) comprises a series of nucleotides, which include Adenine (A), Cytosine (C), Guanine (G), and Uracil (U), linked together by phosphodiester bonds. This series is commonly referred to as the RNA sequence or RNA primary structure [8] (as illustrated in Figure 1.1).

Secondary structure

The secondary structure of an RNA sequence arises when the RNA strand folds on itself, by establishing hydrogen bonds between G-C, A-U, and G-U base pairs [1] (see Figure 1.2). Predicting RNA secondary structure involves determining these hydrogen bonds in an RNA molecule solely from its primary sequence. RNA secondary structure encompasses various elements, including stacked pairs or stems, hairpin loops, multi-branched loops, internal loops, bulge loops, and a more complex components known as a pseudoknot [8].

Tertiary Structure or Three-Dimensional (3D) Structure

The RNA tertiary structure refers to the spatial or three- dimensional organization of RNA components (see Figure 1.3), encompassing helical duplexes, triple-stranded structures, and various components interconnected by a set of interactions known as RNA tertiary interactions [9].

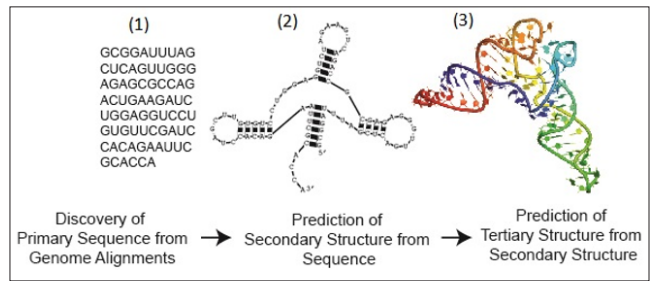
Figure 1: The Three Levels of RNA Structure

RNA Structures Prediction Approaches and Algorithms RNA structures determination plays a vital role in addressing various challenges associated with understanding the RNA physical structure, including deciphering the three-dimensional arrangement and interpreting the biochemical functions of these molecules [5].

The utilization of experimental techniques such as Crystallography, X-Ray, and Nuclear Magnetic Resonance for RNA structure determination necessitates significant financial resources, substantial effort, and a substantial time commitment [6]. In response, bioinformaticians have introduced diverse methods and algorithms as an alternative approach to predict secondary and tertiary structures using various strategies.

In this section, we will shed light on the most commonly used approaches for predicting RNA secondary and tertiary structures.

•  RNA Secondary Structure Prediction

The process of RNA folding is typically hierarchical, with local interactions taking precedence and being energetically more significant than tertiary interactions [10-11]. As a result, the RNA secondary structure serves as a foundational framework for its native 3D structure, and it can be predicted without requiring knowledge of tertiary interactions.

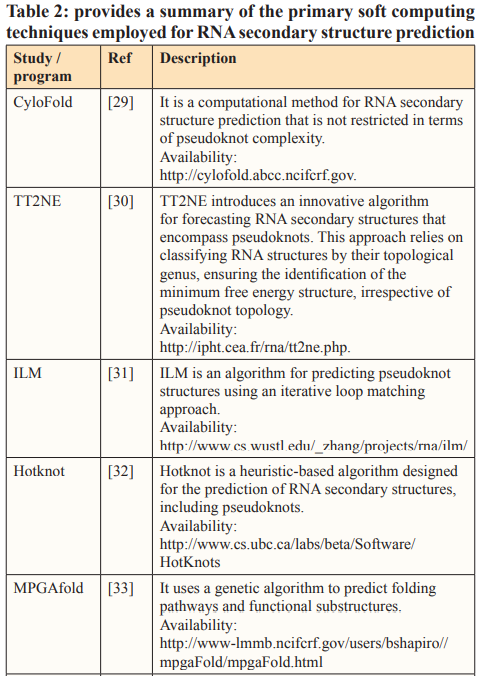
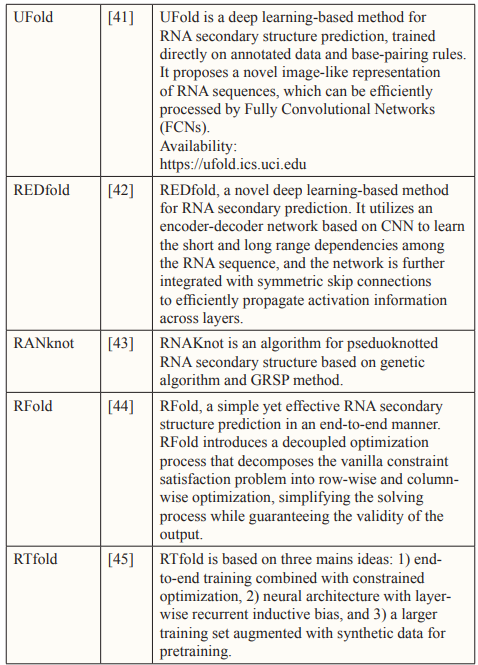
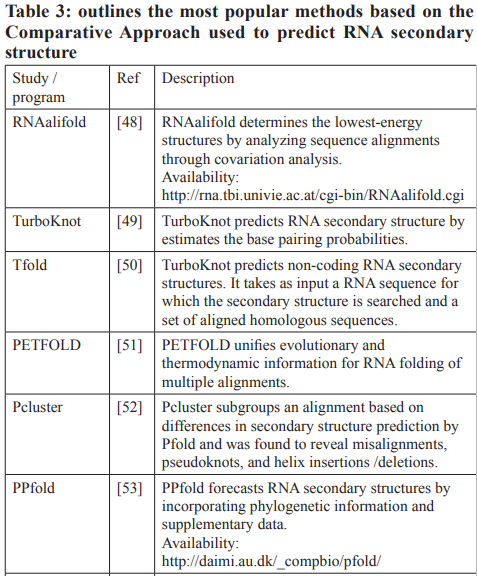
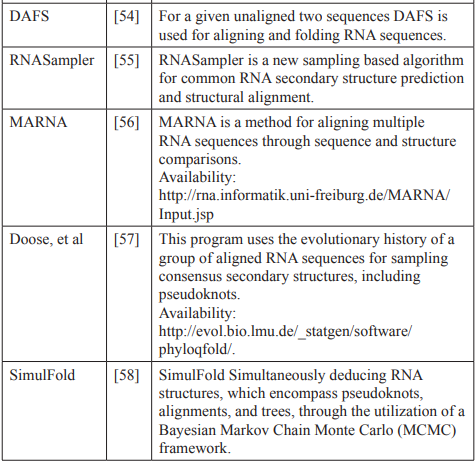
Over the past three decades, numerous methods have been developed for predicting RNA secondary structure. These methods can be categorized into three groups: Dynamic Programming Approach (DPA), Soft Computing (SC), and Comparative Approach (CA). In the subsequent sections, we will offer a concise overview of these approaches.

• Dynamic Programming Approach (DPA)

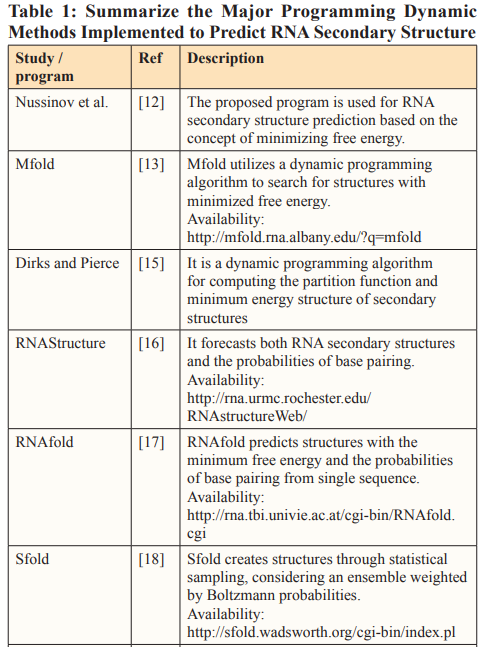
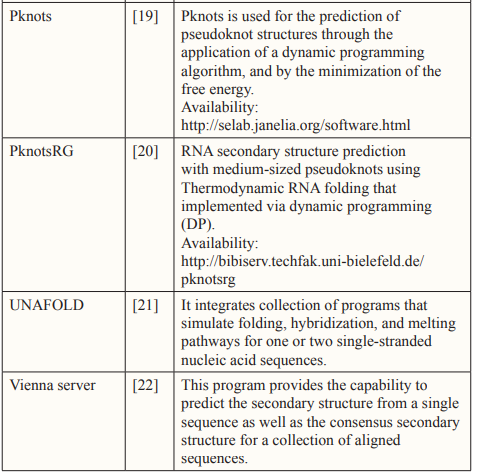
Dynamic Programming (DPA) operates on the concept of breaking down a complex problem into smaller sub problems. By integrating this concept with the principle of minimizing free energy, numerous algorithms have been developed for RNA structure prediction. According to the free energy minimization principle, the structure of an RNA sequence can be the most stable one with the lowest free energy. The most fundamental dynamic programming algorithms generate basic secondary structures without pseudoknot component. Typically, these algorithms face challenges due to their significant time and space complexities [8]. Nussinov et al. introduced the initial algorithm for RNA secondary structure prediction, grounded in the concept of minimizing free energy [12]. The objective of this algorithm is to maximize the number of base pairs to achieve minimal free energy. The computational time complexity for this algorithm is O(n^{^3}). Subsequently, Zuker presented a well-known algorithm, known as Mfold, for predicting RNA secondary structures without considering pseudoknots [13]. This program forecasts secondary structures by minimizing free energy, based on the thermodynamic model proposed by Tinoco in [14].

Soft Computing

Soft Computing (SC) comprises a collection of methods that can be employed either individually or in combination to address various practical challenges. SC methodologies exploit the tolerance of imprecision, uncertainty, approximate reasoning, and partial truths in order to provide cost-effective and optimal solutions [25].

Among of the most commonly utilized SC techniques for RNA structures prediction include Evolutionary Computation, such as Genetic algorithms, and Artificial Neural Networks (ANN).

Genetic Algorithm (GA)

Genetic algorithms (GAs) are dynamic and robust tools founded on the concepts of selection and evolution. GAs are employed to generate multiple solutions for a specific problem [26]. Genetic algorithms become the preferred option when addressing real- world challenges characterized by vast and intricate search spaces, rendering conventional search methods ineffective.

The utilization of Genetic Algorithms (GAs) necessitates the definition of specific operators, including selection, crossover, and mutation. Additionally, a fitness function is essential to assess the quality of each solution. The application of GAs for predicting secondary structures has been explored in numerous studies.

Based on the free energy minimization principle and the RNA folding pathways, Van Batenburg et al. introduce a Genetic Algorithm (GA) for RNA secondary structure prediction [27]. This algorithm commences by creating a list of potential structures, which constitutes the initial population. The operations of crossover and mutation serve as key operators, and two distinct fitness criteria are applied: the summation of stem lengths and the summation of stem stacking energies.

Artificial Neural Networks (ANN)

Artificial Neural Networks (ANNs) represent an information processing system composed of a large number of interconnected processing units often referred to as “neurons.” These neurons work collaboratively to address specific problems. ANNs are designed to tackle artificial intelligence challenges by acquiring knowledge through learning. ANNs also find applications in tasks such as classification, clustering, and prediction [8]. Several studies have explored the use of ANNs for RNA structures prediction.

In reference 28, they introduce a parallel algorithm based on a Hopfield Neural Network (HNN) for the prediction of RNA structures [28]. This method employs the HNN to identify a nearly maximal independent set within an adjacent graph formed by RNA base pairs. Subsequently, it calculates the stable structure of the RNA.

Comparative Approach (CA)

Due to the inherent connection between structure and function, it is reasonable to hypothesize that sequences sharing the same functions should also exhibit similar structures [46]. The comparative approach focuses on searching for conserved regions within the sequences, for this reason, it is employed when dealing with an alignment of sequences from different species that serve the same function. In such cases, CA is deemed more pertinent compared to the dynamic approach that relies on the thermodynamic principle [8].

The initial effective algorithm employing this approach was created by Han and Kim [47]. This algorithm takes a collection of aligned sequences and conducts a phylogenetic comparison, seeking a specific number of the most likely shared structures. It comprises two key phases, with the first step dedicated to the examination of the phylogenetic comparison, while the second step is focused on choosing the most optimal secondary structures.

RNA Tertiary (3D) Structure Prediction

While the secondary structure offers a fundamental outline of an RNA molecule, having knowledge of the RNA’s 3D structure remains essential for gaining a comprehensive understanding of its function. Initially, RNA structure experts successfully constructed 3D structures for common RNA molecules like tRNAs, group II introns, and RNase P [59].

In recent years, various computational methods have been developed to predict RNA 3D structures. These methods can be categorized into three models or approaches, including Knowledge-based approach, physics-based approach, and Deep-Learning-Based approach.

Knowledge-Based Modeling

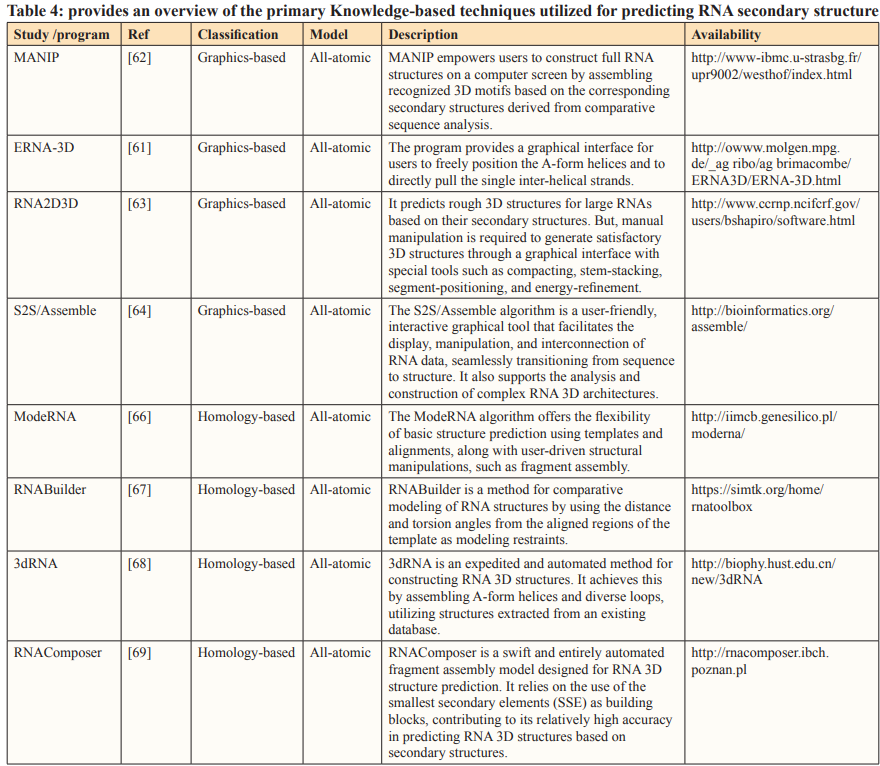
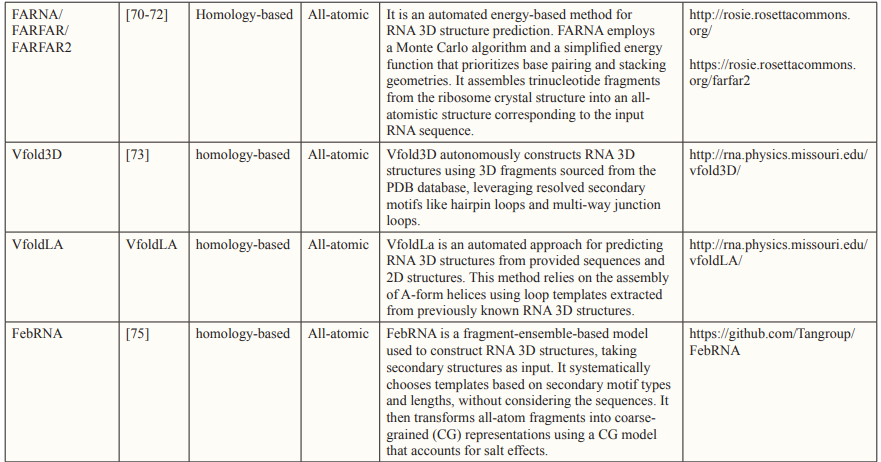
As the number of experimentally determined structures in the database continues to grow, RNA 3D structures can be predicted through the assembly of known motifs or sequence alignment. Knowledge-based modeling primarily encompasses graphic-based modeling and homology-based modeling [60].

Graphics-Based Methods

Graphical modeling typically offers a graphical interface, enabling users to create RNA 3D structures through the manipulation or assembly of RNA segments. The primary graphical-based algorithms include, ERNA-3D, MANIP, RNA2D3D, S2S/Assemble [61-64].

Homology-Based Methods

Given that the 3D structure of a macromolecule evolves at a much slower rate than its sequence, evolutionarily related macromolecules typically maintain similar 3D structures even when their sequences diverge. Leveraging this observation, the 3D structures of a macromolecule can be constructed by aligning the sequence of the target molecule with the structures of template molecules.

Comparative modeling, which is also known as homology-based modeling or template-based modeling, has proven to be quite effective in predicting the 3D structures of proteins. Similarly, in the context of RNA 3D structure prediction, several algorithms, including Mode RNA [66], RNA Builder, and 3Drna, have been created for constructing RNA 3D structures [65-68].

Physics-BasedModeling

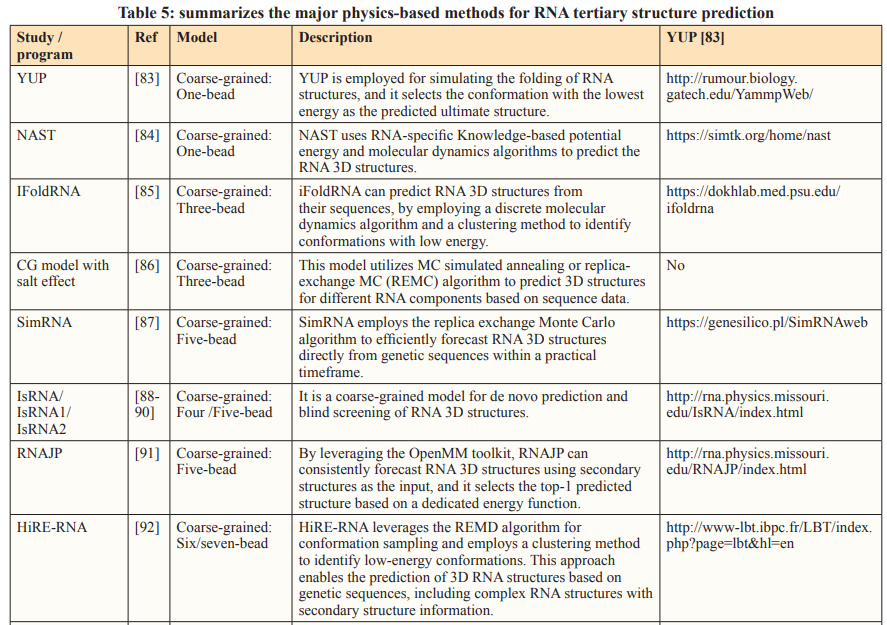
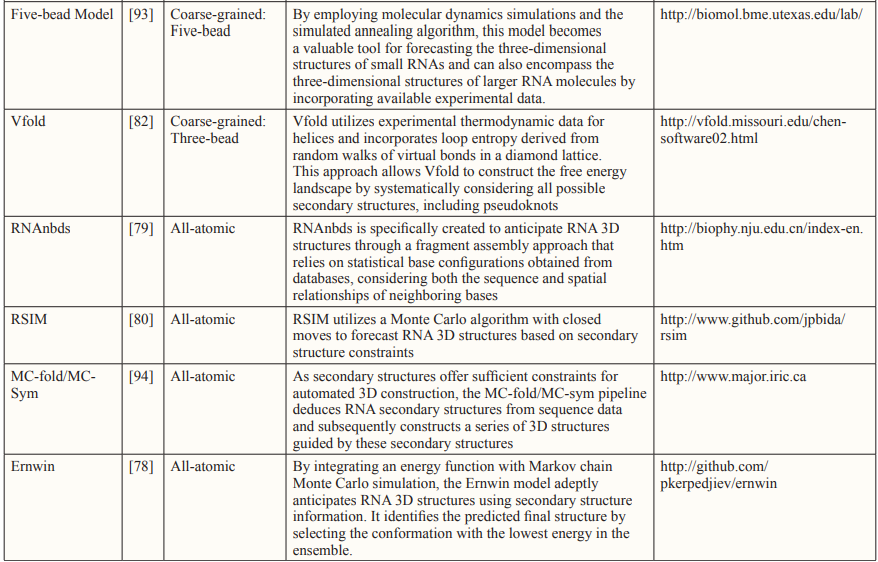
Physics-based methods rely on biophysical principles to simulate the folding process, aiming to find a conformation with the lowest free energy. Given that modeling a full-atom RNA structure typically entails numerous degrees of freedom and, consequently, significant computational complexity, various coarse-grained predictive models have been introduced at different resolution levels, incorporating physical simplifications [59].

All-Atomistic Model

Traditionally, all-atomistic molecular dynamics using physics-based atomic force fields like CHARMM and AMBER have been widely employed for macromolecular modeling, offering insights into the actual movements of atoms [7]. However, the challenge of folding RNA 3D structures persists due to the numerous degrees of freedom, even with the most advanced computational resources [5]. Consequently, models that assemble all-atomistic fragments based on known fragments or secondary structures have been developed, as exemplified by the Ernwin, RNAnbds and RSIM [76-80].

Coarse-Grained Model

An alternative approach to reduce computational costs involves reducing the number of particles by considering a cluster of functional atoms as a single bead. The size of this bead can vary, representing either a small group of atoms or a larger assembly, depending on the model’s resolution [5]. After the initial development of the one-bead RNA model by Malhotra and Harvey, numerous coarse- grained (CG) models have been introduced to predict RNA 3D structures or to model interactions between RNAs and other molecules, examples of which include Vfold, YUP and NAST [81- 84].

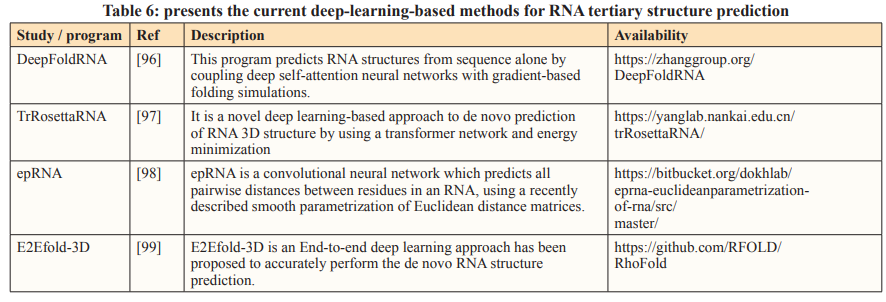
TheDeep-Learning-Based Approaches

The rise of artificial intelligence has made significant strides in advancing science and technology worldwide in recent years. Building upon the success of deep learning in protein 3D structure prediction, some deep-learning-based methods have emerged for predicting RNA 3D structures, albeit facing the challenge of limited RNA structural data in the PDB database when compared to proteins [95]. Nevertheless, it is important to acknowledge that achieving precise predictions of macromolecule 3D structures often hinges on the availability of extensive experimental structural data.

Conclusion

As comprehending RNA structures, particularly in three dimensions, holds vital significance in unraveling the enigmatic RNA world, there has been a surge in the development of computational models for RNA structure modeling in recent years.

Predicting RNA secondary structures is comparatively more manageable through techniques like sequence alignment, thermodynamics-based dynamic programming algorithms, or a combination thereof. Enhancing the accuracy of such predictions can be achieved through expanding structural databases or refining empirical thermodynamic parameters. However, the field of RNA 3D structure prediction is still in its early stages and confronts several challenges. Nonetheless, recent achievements in RNA 3D structure modeling offer promising prospects for exciting advancements in RNA structure prediction in the upcoming decade.

References

1. Crick F (1970) Central dogma of molecular Nature 227: 561-563.
2. Griffiths-Jones S, Moxon S, Marshall M, Khanna A, Eddy SR, et (2005) Rfam: annotating non-coding RNAs in complete genomes. Nucleic Acids Research 33: 121-124.
3. Doherty EA, Doudna JA (2001) Ribozyme structures and Annual review of biophysics and biomolecular structure 30: 457-475.
4. Edwards TE, Klein DJ, Ferré-D’Amaré AR (2007) Riboswitches: small-molecule recognition by gene regulatory Current opinion in structural biology 17: 273-279.
5. Wang X, Yu S, Lou E, Tan YL, Tan ZJ (2023) RNA 3D Structure Prediction: Progress and Perspective. Molecules 28: 5532.
6. Osman MN, Abdullah R, Abdul Rashid N (2010) RNA secondary structure prediction using dynamic programming algorithm-a review and proposed work. In: 2010 International Symposium in Information Technology 2: 551-556.
7. Sponer J, Bussi G, Krepl M, Banas P, Bottaro S, et al. (2018) RNA structural dynamics as captured by molecular simulations: a comprehensive overview. Chemical reviews118: 4177-4338.
8. El Fatmi A, Chentoufi A, Bekri MA, Benhlima S, Sabbane M (2018) RNA secondary structure an In Innovations in Smart Cities and Applications: Proceedings of the 2nd Mediterranean Symposium on Smart City Applications Springer International Publishing 2: 379-388.
9. Butcher SE, Pyle AM (2011) The molecular interactions that stabilize RNA tertiary structure: RNA motifs, patterns, and networks. Accounts of chemical research 44: 1302-1311.
10. Tinoco Jr I, Bustamante C (1999) How RNA Journal of molecular biology 293: 271-281.
11. Laing C, Schlick T (2010). Computational approaches to 3D modeling of RNA. Journal of Physics: Condensed Matter 22: 283101.
12. Nussinov R, Pieczenik G, Griggs JR, Kleitman DJ (1978) Algorithms for loop matchings. SIAM Journal on Applied mathematics 35: 68-82.
13. Zuker M (2003) Mfold web server for nucleic acid folding and hybridization prediction. Nucleic acids research 31: 3406-3415.
14. Tinoco I, Borer PN, Dengler B, Levine MD, Uhlenbeck OC, et al. (1973) Improved estimation of secondary structure in ribonucleic acids. Nature New Biology 246: 40-41.
15. Dirks RM, Pierce NA (2003) A partition function algorithm for nucleic acid secondary structure including Journal of computational chemistry 24: 1664-1677.
16. Reuter JS, Mathews DH (2010) RNAstructure: software for RNA secondary structure prediction and BMC bioinformatics 11: 1-9.
17. Hofacker IL, Stadler PF (2006). Memory efficient folding algorithms for circular RNA secondary structures. Bioinformatics 22: 1172-1176.
18. Ding Y, Lawrence CE (2003) A statistical sampling algorithm for RNA secondary structure prediction. Nucleic acids research 31: 7280-7301.
19. Rivas E, Eddy SR (1999) A dynamic programming algorithm for RNA structure prediction including Journal of molecular biology 285: 2053-2068.
20. Reeder J, Giegerich R (2004) Design, implementation and evaluation of a practical pseudoknot folding algorithm based on thermodynamics. BMC bioinformatics 5: 1-12.
21. Markham NR, Zuker M (2008) UNAFold: software for nucleic acid folding and hybridization. Bioinformatics: structure, function and applications 453: 3-31.
22. Hofacker IL (2003) Vienna RNA secondary structure Nucleic acids research 31: 3429-3431.
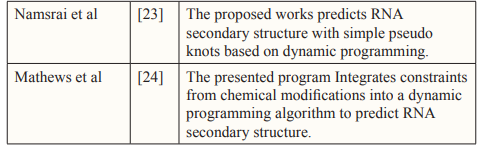
23. Namsrai OE, Jung KS, Kim S, Ryu KH (2006) RNA secondary structure prediction with simple pseudoknots based on dynamic programming. In International Conference on Intelligent Computing 4115: 303-311.
24. Mathews DH, Disney MD, Childs JL, Schroeder SJ, Zuker M, et (2004). Incorporating chemical modification constraints into a dynamic programming algorithm for prediction of RNA secondary structure. Proceedings of the National Academy of Sciences 101: 7287-7292.
25. Ray SS, Pal SK (2012) RNA secondary structure prediction using soft computing. IEEE/ACM Transactions on computational biology and bioinformatics 10: 2-17.
26. Holland JH (1962) Outline for a logical theory of adaptive systems. Journal of the ACM (JACM) 9: 297-314.
27. Van Batenburg FHD, Gultyaev AP, Pleij CW (1995) An APL-programmed genetic algorithm for the prediction of RNA secondary structure. Journal of theoretical Biology 174: 269-280.
28. Liu Q, Ye X, Zhang Y (2006) A Hopfield neural network based algorithm for RNA secondary structure prediction. In First International Multi-Symposiums on Computer and Computational Sciences (IMSCCS’06) 1: 10-16.
29. Bindewald E, Kluth T, Shapiro BA (2010) CyloFold: secondary structure prediction including pseudoknots. Nucleic acids research 38: W368-W372.
30. Bon M, Orland H (2011) TT2NE: a novel algorithm to predict RNA secondary structures with Nucleic acids research 39: e93.
31. Ruan J, Stormo GD, Zhang W (2004) An iterated loop matching approach to the prediction of RNA secondary structures with pseudoknots. Bioinformatics 20: 58-66.
32. Ren J, Rastegari B, Condon A, Hoos HH (2005) HotKnots: heuristic prediction of RNA secondary structures including pseudoknots. Rna 11: 1494-1504.
33. Shapiro BA, Wu JC, Bengali D, Potts MJ (2001) The massively parallel genetic algorithm for RNA folding: MIMD implementation and population variation. Bioinformatics 17: 137-148.
34. Geis M, Flamm C, Wolfinger MT, Tanzer A, Hofacker IL, et al. (2008) Folding kinetics of large RNAs. Journal of molecular biology 379: 160-173.
35. Giegerich R, Voß B, Rehmsmeier M (2004) Abstract shapes of RNA. Nucleic acids research 32: 4843-4851.
36. Koessler DR, Knisley DJ, Knisley J, Haynes T (2010) A predictive model for secondary RNA structure using graph theory and a neural In BMC bioinformatics 11: 1-10.
37. Shapiro BA, Navetta J (1994). A massively parallel genetic algorithm for RNA secondary structure prediction. The Journal of Supercomputing 8: 195-207.
38. Wiese K, Deschenes A, Hendriks A (2008) RnaPredict— an evolutionary algorithm for RNA secondary structure prediction. IEEE/ACM Transactions on Computational Biology and Bioinformatics 5: 25-41.
39. Tong KK, Cheung KY, Lee KH, Leung KS (2013) GAknot: RNA secondary structures prediction with pseudoknots using Genetic Algorithm. https://ieeexplore.ieee.org/document/6595399.
40. Zou Q, Zhao T, Liu Y, Guo M (2009) Predicting RNA secondary structure based on the class information and Hopfield network. Computers in Biology and Medicine 39: 206-214.
41. Fu L, Cao Y, Wu J, Peng Q, Nie Q, et (2022) UFold: fast and accurate RNA secondary structure prediction with deep learning. Nucleic acids research 50: e14.
42. Chen CC, Chan YM (2023) REDfold: accurate RNA secondary structure prediction using residual encoder-decoder BMC bioinformatics 24: 1-13.
43. El Fatmi A, Bekri MA, Benhlima S (2019) RNAknot: A new algorithm for RNA secondary structure prediction based on genetic algorithm and GRASP method. Journal of bioinformatics and computational biology 17: 1950031.
44. Tan C, Gao Z, Li SZ (2022) Rfold: Towards simple yet effective RNA secondary structure https://arxiv.org/abs/2212.14041.
45. Jung AJ, Lee LJ, Gao AJ, Frey BJ (2022). RTfold: RNA secondary structure prediction using deep learning with domain inductive https://icml-compbio.github.io/icml-website-2022/2022/papers/WCBICML2022_paper_38.pdf.
46. Engelen S, Tahi F (2007) Predicting RNA secondary structure by the comparative approach: how to select the homologous sequences. BMC bioinformatics 8: 1-12.
47. Han K, Kim HJ (1993) Prediction of common folding structures of homologous RNAs. Nucleic Acids Research 21: 1251-1257.
48. Bernhart SH, Hofacker IL, Will S, Gruber AR, Stadler PF (2008) RNAalifold: improved consensus structure prediction for RNA alignments. BMC bioinformatics 9: 1-13.
49. Seetin MG, Mathews DH (2012). TurboKnot: rapid prediction of conserved RNA secondary structures including Bioinformatics 28: 792-798.
50. Engelen S, Tahi F (2010) Tfold: efficient in silico prediction of non-coding RNA secondary Nucleic acids research 38: 2453-2466.
51. Seemann SE, Gorodkin J, Backofen R (2008). Unifying evolutionary and thermodynamic information for RNA folding of multiple Nucleic Acids Research 36: 6355-6362.
52. Andersen ES, Lind Thomsen A, Knudsen B, Kristensen SE, Havgaard JH, et (2007) Semiautomated improvement of RNA alignments. RNA 13: 1850-1859.
53. Sükösd Z, Knudsen B, Værum M, Kjems J, Andersen ES (2011) Multithreaded comparative RNA secondary structure prediction using stochastic context-free grammars. BMC bioinformatics 12: 1-8.
54. Sato K, Kato Y, Akutsu T, Asai K, Sakakibara Y (2012) DAFS: simultaneous aligning and folding of RNA sequences via dual Bioinformatics 28: 3218-3224.
55. Xu X, Ji Y, Stormo GD (2007) RNA Sampler: a new sampling based algorithm for common RNA secondary structure prediction and structural alignment. Bioinformatics 23: 1883-1891.
56. Siebert S, Backofen R (2005) MARNA: multiple alignment and consensus structure prediction of RNAs based on sequence structure comparisons. Bioinformatics 21: 3352-3359.
57. Doose G, Metzler D (2012) Bayesian sampling of evolutionarily conserved RNA secondary structures with pseudoknots. Bioinformatics 28: 2242-2248.
58. Meyer IM, Miklós I (2007) SimulFold: simultaneously inferring RNA structures including pseudoknots, alignments, and trees using a Bayesian MCMC framework. PLoS computational biology 3: e149.
59. Shi YZ, Wu YY, Wang FH, Tan ZJ (2014) RNA structure prediction: progress and Chinese Physics B 23: 078701.
60. Ou X, Zhang Y, Xiong Y, Xiao Y (2022) Advances in RNA 3D structure Journal of Chemical Information and Modeling 62: 5862-5874.
61. Zwieb C, Müller F (1997) Three-dimensional comparative modeling of RNA. In Nucleic acids symposium series 36: 69-71.
62. Massire C, Westhof E (1998) MANIP: an interactive tool for modelling RNA. Journal of Molecular Graphics and Modelling 16: 197-205.
63. Martinez HM, Maizel Jr JV, Shapiro BA (2008) RNA2D3D: a program for generating, viewing, and comparing 3-dimensional models of RNA. Journal of Biomolecular Structure and Dynamics 25: 669-683.
64. Jossinet F, Westhof E (2005) Sequence to Structure (S2S): display, manipulate and interconnect RNA data from sequence to structure. Bioinformatics 21: 3320-3321.
65. Zhang Y, Skolnick J (2013) Segment assembly, structure alignment and iterative simulation in protein structure prediction. BMC biology 11: 1-4.
66. Rother M, Rother K, Puton T, Bujnicki JM (2011) ModeRNA: a tool for comparative modeling of RNA 3D Nucleic acids research 39: 4007-4022.
67. Flores SC, Altman RB (2010) Turning limited experimental information into 3D models of RNA. Rna 16: 1769-1778.
68. Zhao Y, Huang Y, Gong Z, Wang YJ, Man JF, et (2012) Automated and fast building of three-dimensional RNA structures. Sci Rep 2: 734.
69. Popenda M, Szachniuk M, Antczak M, Purzycka KJ, Lukasiak P, et (2012) Automated 3D structure composition for large RNAs. Nucleic 807 Acids Res 40: e112.
70. Das R, Baker D (2007) Automated de novo prediction of native-like RNA tertiary structures. Proceedings of the National Academy of Sciences 104: 14664-14669.
71. Das R, Karanicolas J, Baker D (2010) Atomic accuracy in predicting and designing noncanonical RNA Nature methods 7: 291-294.
72. Watkins AM, Rangan R, Das R (2020) FARFAR2: improved de novo rosetta prediction of complex global RNA folds. Structure 28: 963-976.
73. Cao S, Chen SJ (2011) Physics-based de novo prediction of RNA 3D The journal of physical chemistry B 115: 4216-4226.
74. Xu X, Chen SJ (2017) Hierarchical assembly of RNA three- dimensional structures based on loop The Journal of Physical Chemistry B 122: 5327-5335.
75. Zhou L, Wang X, Yu S, Tan YL, Tan ZJ (2022) FebRNA: An automated fragment-ensemble-based model for building RNA 3D structures. Biophysical Journal 121: 3381-3392.
76. Brooks BR, Brooks III CL, Mackerell Jr AD, Nilsson L, Petrella RJ, et al. (2009). CHARMM: the biomolecular simulation program. Journal of computational chemistry 30: 1545-1614.
77. Case DA, Cheatham III TE, Darden T, Gohlke H, Luo R, et al. (2005) The Amber biomolecular simulation programs. Journal of computational chemistry 26: 1668-1688.
78. Kerpedjiev P, Zu Siederdissen CH, Hofacker IL (2015) Predicting RNA 3D structure using a coarse-grain helix- centered model. Rna 21: 1110-1121.
79. Zhang J, Bian Y, Lin H, Wang W (2012). RNA fragment modeling with a nucleobase discrete-state model. Physical Review E 85: 021909.
80. Bida JP, Maher LJ (2012) Improved prediction of RNA tertiary structure with insights into native state dynamics. RNA 18: 385-393.
81. Malhotra A, Harvey SC (1994) A quantitative model of the Escherichia coli 16 S RNA in the 30 S ribosomal subunit. Journal of molecular biology 240: 308-340.
82. Cao S, Chen SJ (2005) Predicting RNA folding thermodynamics with a reduced chain representation Rna 11: 1884-1897.
83. Tan RK, Petrov AS, Harvey SC (2006). YUP: A molecular simulation program for coarse-grained and multiscaled models. Journal of chemical theory and computation 2: 529-
84. Jonikas MA, Radmer RJ, Laederach A, Das R, Pearlman S, et al. (2009) Coarse-grained modeling of large RNA molecules with knowledge-based potentials and structural filters. Rna 15: 189-199.
85. Ding F, Sharma S, Chalasani P, Demidov VV, Broude NE, et al. (2008) Ab initio RNA folding by discrete molecular dynamics: from structure prediction to folding Rna 14: 1164-1173.
86. Shi YZ, Wang FH, Wu YY, Tan ZJ (2014) A coarse-grained model with implicit salt for RNAs: predicting 3D structure, stability and salt effect. The Journal of chemical physics 141: 105102.
87. Boniecki MJ, Lach G, Dawson WK, Tomala K, Lukasz P, et al. (2016) Sim RNA: a coarse-grained method for RNA folding simulations and 3D structure prediction. Nucleic acids research 44: e63.
88. Zhang D, Chen SJ (2018) IsRNA: An iterative simulated reference state approach to modeling correlated interactions in RNA Journal of chemical theory and computation 14: 2230-2239.
89. Zhang, D, Li J, Chen SJ (2021) IsRNA1: de novo prediction and blind screening of RNA 3D Journal of chemical theory and computation 17: 1842-1857.
90. Zhang D, Chen SJ, Zhou R (2021) Modeling noncanonical RNA base pairs by a coarse-grained IsRNA2 model. The Journal of Physical Chemistry B 125: 11907-11915.
91. Li J, Chen SJ (2023) RNAJP: enhanced RNA 3D structure predictions with non-canonical interactions and global topology Nucleic Acids Research 51: 3341-3356.
92. Cragnolini T, Laurin Y, Derreumaux P, Pasquali S (2015) Coarse-grained HiRE-RNA model for ab initio RNA folding beyond simple molecules, including noncanonical and multiple base pairings. Journal of chemical theory and computation 11: 3510-3522.
93. Xia Z, Gardner DP, Gutell RR, Ren P (2010) Coarse-grained model for simulation of RNA three-dimensional The Journal of Physical Chemistry B 114: 13497-13506.
94. Parisien M, Major F (2008) The MC-Fold and MC-Sym pipeline infers RNA structure from sequence data. Nature 452: 51-55.
95. Zhao Q, Zhao Z, Fan X, Yuan Z, Mao Q, et (2021) Review of machine learning methods for RNA secondary structure prediction. PLoS computational biology 17: e1009291.
96. Pearce R, Omenn GS, Zhang Y (2022) De novo RNA tertiary structure prediction at atomic resolution using geometric potentials from deep https://www.biorxiv.org/cont ent/10.1101/2022.05.15.491755v1.
97. Feng C, Wang W, Han R, Wang Z, Ye L, et (2022) Accurate de novo prediction of RNA 3D structure with transformer network. https://www.biorxiv.org/content/10.1101/2022.10.24.513506v1.full.pdf.
98. Congzhou MS, Wang J, Dokholyan NV (2023) Predicting 3D RNA structure from solely the nucleotide sequence using Euclidean distance neural networks. Biophysical Journal 122: 444a.
99. Shen T, Hu Z, Peng Z, Chen J, Xiong P, et al. (2022) E2Efold-3D: end-to-end deep learning method for accurate de novo RNA 3D structure prediction. https://arxiv.org/abs/2207.01586.

View PDF

Our Pubmed Indexed Articles

---

---

---