Author(s): SOA Olawale, OP Akintunde*, MO Afolabi and OA Agbede
This paper presents the Fuzzy logics approach for a singly reinforced concrete beam. The rules are generated for the FIS for the variables. The width, and the moment constitutes the crisp data for the inputs and the steel ratio represents the crisp output. The MATLAB fuzzy tool kit is used to execute the simulation. The code prescription of the design of a singly reinforced concrete beam is a straight forward calculation. However, the overestimation of reinforcement can be enormous. This can be very impacting on the cost of the project. This work attempts to use fuzzy logic predictive power to design a singly reinforced concrete beam. The result reasonable agreement between the code provisions and the fuzzy logic predictions. It was established that fuzzy logic can be adopted as a significant technique for the optimization of the design of a singly reinforced concrete beam.
Reinforced concrete is used globally today to make several structures including high rise buildings, tunnels, canals, reservoirs, foundations, retaining walls, bridges, etc. reinforced concrete is usually cost-effective as compared to other structural materials such as steel, wood, etc. and also possess qualities like high fire resistance, compressive strength, shape or sections flexibilities for members suitable for all manners of sections that satisfy the architectural requirements. All these are responsible for the widespread applications of reinforced concrete. Several methods of design and analysis can be adopted for reinforced concrete members like columns, beams, slabs, shear walls, etc. of which soft computing is one. Soft computing outputs are impulsive, unsure, and have values settling between 0 and 1. These features made an official aspect of review in computer science since the early parts of the 1990s. Relatively simple systems only can be analysed and modelled precisely in early computational procedures. In many fields such as sciences, biology, medicine, humanities etc., more sophisticated methods arising with normal mathematical and analytical means are difficult and come with a high computational cost to produce dependable, viable, and verifiable results. Reduced calculation errors and more accurate and reliable solutions of complex problems are obtained with the aids of soft computing tools or artificial intelligence design applications. One of the key components of soft computing or artificial intelligence tools is Fuzzy logic. The terminology was first introduced in 1965 by Zadeh with the proposal of a fuzzy set theory. Fuzzy logic is a method of many-valued judgment and reason that deals with estimated or approximated parameters instead of static and fixed reasoning [1-5].
Zadeh projected the term soft computing and was also the one who introduced the fuzzy logic. He defines it as follows: ?Soft computing is a collection of methodologies that aim to exploit the tolerance for imprecision and uncertainty to achieve tractability, robustness, and low solution cost. Its principal constituents are fuzzy logic, neurocomputing, and probabilistic reasoning. Soft computing is likely to play an increasingly important role in many application areas, including software engineering. The role of the model for soft computing is the human mind [6]. One of the Artificial Intelligent Techniques used for transferring human inexact skills to generate a readable pattern for machines and computers is the Soft Computing and Fuzzy Logic (M G Simoes).
The four main components of each fuzzy system are Fuzzification, Fuzzy rule base, Inference Engine, and Defuzzification.
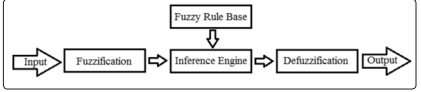
Figure 1: Flowchart of Fuzzy Logic
The first component that estimates the fuzzy input and process them into one or more fuzzy sets is the Fuzzification. The two kinds of Fuzzifications are Gaussian and Trapezoidal. Any item can belong to various subsets of universal set in that type of fuzzy logic. Linguistic IF-THEN-constructions that have the total method ?IF A THEN B? where A and B are schemes involving linguistic variables are the Fuzzy rules base. A is named the premise and B is named the significance of the rule. Consequently, the use of linguistic variables and fuzzy IF-THEN-rules adventures the allowance for inaccuracy and ambiguity. There are two kinds of rules methods depending on the uniqueness of the problems. Fuzzy rule base is being involved and merged in the analysis of fuzzy outputs in a fuzzy inference engine. Outputs are being taken from a fuzzy inference engine and then converted to accurate numerical values and a crisp output by the Defuzzification. Fa-Liang studied a new way of predicting cement strength- fuzzy logic in 1997. He analysed the fuzzy logic system and estimated six samples with fuzzy models and then submitted that fuzzy logic is the new method for estimating cement strength and new applying span for the fuzzy concept. Akkurt et al. (2004) studied the Fuzzy logic model for the calculation of cement compressive strength [7-10]. Alkali, Blaine, SO3, and C3S were all observed as inputs variables and obtained 28-day compressive strength as the output variable and then fuzzified those using Artificial Neural Networks (ANNs).
The cement strength studied was compared with the predicted values using the fuzzy model. It was concluded that fuzzy logic application compared favourably with ANNs and was more unambiguous and vital. Tesfamariam and Najjaran (2007) studied the adaptive network-fuzzy inferencing to predict concrete strength using mix design [11]. Adaptive neuro-fuzzy inference system (ANFIS), was adopted offering the addition of learning, flexibility method for resolving critical problems (Moreno-Velo et al 2003) [12,16]. Concrete slump in cm, water-cement ratio (w/c), fa percentage (%), ca percentage (%) and admixture (%) were used as input variables and real samples data of concrete mix proportions of two companies as models A & B were used to obtain these data. The result of the predicted strength of cement as r2 values was reported. The corresponding absolute and relative model coefficients of determination, values of r2 are Model A (0.999, 0.984), Model B (0.970, 0.995), and Model A-B (0.999, 0.998) were obtained. This shows a successful output of the fuzzy Logic.
The compressive strength of self-compacting concrete at 28 days was predicted using fuzzy logic and the outcome results were reported to be within 20% perfect agreement [13-15]. Sixty samples gotten from selected pieces of literature were used for the analysis. Triangular membership function spanning from four to nine was used with the Sugeno type fuzzy inference method. One of the possible areas of concern was the data set used by the reviewers. The source of disagreement in the final outputs in the properties of the variations of the constituent materials arose from the fact that the data was gotten from four different authors. Root mean square error was 5.626 and the mean absolute error was 4.885. The accurate outcome of the compressive strength model was effectively produced using the Sugeno type FIS. The data source was a mixture of various sets with probable varying testing scenarios; hence, the model could not be further accurate. MATLAB®: fuzzy toolboxes and MATLAB®: Simulink option is used in the application of fuzzy logic. Simulink®: provides the environment for multi-domain reproduction or simulation and Model-Based Design for varying and enclosed systems. It also allows for a collaborative environment and personalized set of block libraries that enable you to design, model, activate, and examine various multiple systems which include interactions, controls, signal processing, video processing, and image processing.
The materials required to prospect the present work are excel and MATLAB software. The provisions of EC2 are implemented in the excel spreadsheet calculations to generate training data for the network. The four linguistic variables considered in the work are width, depth, moment, and steel ratio. Each of these variables is mapped to membership functions. The inputs are width, depth, and moment while the output is steel ratio. The triangular membership functions are used for all the variables over ranges of values. The rules are developed for the FIS for the variables. The crisp data are the width, and the moment for the inputs while the steel ratio is the crisp output. The MATLAB fuzzy tool kit is used to implement the simulation. Figures 2 to 8 show the setting up of the MATLAB fuzzy solution to the problem. Figure 2 shows the starting page of the fuzzy solution and figures 3 to 5 are the membership function definitions for the three inputs while figure 6 is the membership function for the steel ratio output variable while figures 7 and 8 are the rules for the FIS engine. The membership functions are clustered based on three hundred data sets and the clustering is between two and five membership functions. The rule is IF (antecedent) THEN (consequents). Samples of the rules are shown in figure 7 and they are presented in the pictorial forms in figure 8.
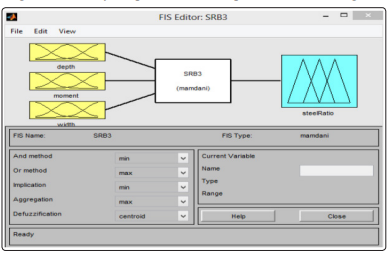
Figure 2: The fuzzy logic tool representation of the design
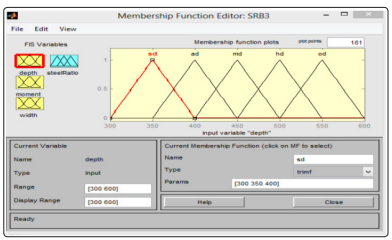
Figure 3: Membership functions for the depth (input)
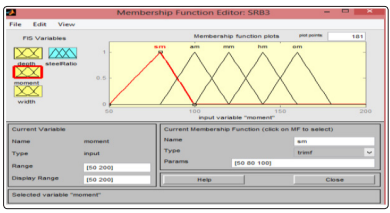
Figure 4: Membership function for moment (input)
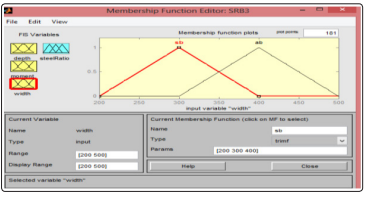
Figure 5: Membership functions for width of the beam (input)
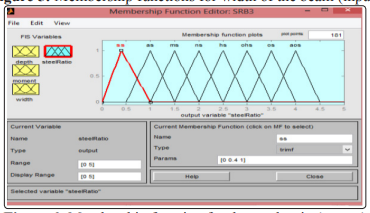
Figure 6: Membership function for the steel ratio (output)
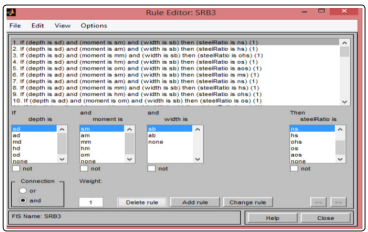
Figure 7: Rules in linguistic form for the inference engine of the FIS

Figure 8: The fuzzy logic rules for the inference engine in diagrammatic form
The results of the computations are presented in figures 9 to 13. The steel ratio decreases with an increase in the width of the beam which in line with the expected behavior as stipulated by the theoretical standing of the beam in flexure. This is reflected in most cases except the flip at the boundary due to numerical noise. The same is true for the depth behavior as shown in figure 10. The moment variation is in contrast to this behavior as shown in figure 11. The more the moment the more the required steel.

Figure 9: Variation of steel ratio with width of the beam
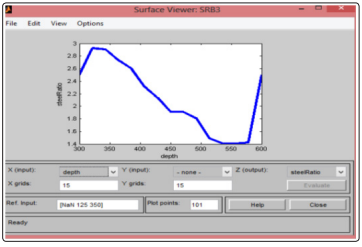
Figure 10: Variation of steel ratio with depth

Figure 11: Variation of steel ratio with moment
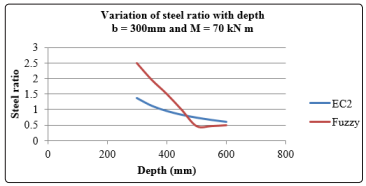
Figure 12: Variation of steel ratio with depth

Figure 13: Variation of steel ratio with moment
The fuzzy logic is demonstrated to be accurate enough to predict the steel requirements of a singly reinforcement concrete beam and this is shown to be safer than EC2 recommendations at the expense of economy as shown clearly in figures 12 and 13. Both figures are the parametric study that compare the fuzzy logic outputs with the EC2 results. The fuzzy logic outputs with the depth shows an improved variation compared to EC2 results. However, the moment effect in fuzzy logic appears to be consistently more steel requirement with a moment than the EC2 computation. The reason for this may be as a result of the membership function ranges adopted. With better refinement of membership functions, there is a likelihood of better convergence. Actually, fuzzy logic outputs show a safer design in the parametric studies. Further works could exploit the use of other membership functions such as Trapezoidal and Gaussian functions.
