“Probabilistic Landslide Hazard Methodology, an Application to a Susceptible Area to Landslides in Colombia”

---

Author(s): Jairo E Yepes-Heredia

Abstract

A Probabilistic method was previously used to perform Probabilistic Hazard Zonation in El Salvador using a new proposed probabilistic methodology (Rodriguez, Yepes 2011). The current project is a case study that uses the same methodology and tries to cover the limitations of the previous and first application, and applied to two historically unstable landslides in Pipiral, an unstable area in the Central Region of Colombia. The susceptibility angle was used as the susceptibility function. Rainfall and earthquakes are considered as landslides triggers. Besides zonation, modeling was performed because the probability model was initially designed to do the zonation of larger areas. A database from “four countries in Central-America and Colombia” of Rainfall Induced Landslides in Fine-grained soils and a database of “historic and worldwide” Earthquake Induced Landslides, were considered to support the model. The intensity-duration-frequency (I-D-F) curves for the Pipiral-Colombia were used to define the probability of occurrence of the critical rainfall, and the seismic hazard analysis of the same area was used to define the probability of occurrence of the critical earthquake.

Introduction

The approach to the problem of evaluating landslide hazard via strictly quantitative methods does not have as many references as semi quantitative and qualitative methods. Then, when it is about considering rainfall and earthquakes as triggers of landslides, it is even more difficult to find valid and available references. Several authors have developed methods that propose methodologies to evaluate landslide hazard. Mora & Vahrson (1994) for instance, developed a model in Costa Rica, to easily and in a practical form, classify landslide risk in seismically active regions, presenting a guide that allows the engineer to take fast decisions considering five factors: slope, lithology, soil moisture, rainfall, and factors of seismic intensity. Rodriguez, Torres & Leon (2004) determined landslide hazard via a probabilistic method applied to destructive seismic events up to 2004 in El Salvador using earthquakes as triggering factor and rainfall and slope angle as susceptibility factors. Rodriguez & Yepes (2009) also worked in El Salvador using rainfall and earthquakes as triggering factors and slope angle as the only susceptibility factor due to the lack of geomechanical properties information that cover all the area. This last research used a probabilistic model that considers the occurrence of rainfall and earthquakes simultaneously but defining that only one of them will trigger the landslide. This limitation is tried to be covered by the current research. The probabilistic methodology was used to perform landslide hazard zonation and two-dimensional modeling using geomechanical properties close to surface was made to consider scale differences. The probabilistic model was initially developed to study large areas like countries. Throughout this paper, both zonation and modeling are carried out considering surface properties. This is because the intention is to analyze how earthquakes and rainfall can trigger landslides. The main intention of this paper is to contribute and to encourage civil engineers to use probability in geotechnical engineering and to raise awareness about the need to work with numerical methodologies for the assessment of landslide hazard instead of using qualitative methods that do not actually give precise results [1-5].

General Setting

To work with probability calculations and with the intention to include variables that can affect slope stability, this work included: seismic parameters, rainfall parameters, the slope angle as a susceptibility value for landslide hazard zonation, and surface friction angle for two-dimensional analysis. Topography, seismicity, and rainfall information for the two landslides studied in the current research project, were provided by SGC “Colombian Geological Survey” and by IDEAM “Institute of Hydrology, Meteorology and Environmental studies” in Colombia. Two databases were updated:

• A worldwide historical database of earthquake-induced landslides, prepared by Rodriguez (1767 B.C. - 2002) and Yepes (2002 - 2007), was updated by Mosquera and Mosquera from 2009 to 2019.
• A historical database of rainfall induced landslides in four countries of Central America (Guatemala, El Salvador, Nicaragua, and Honduras) and Colombia prepared by Yepes (1982 - 2007) was updated by Mosquera and Mosquera from 2009 to 2019.

A short description of the variables involved in the probability model and the calculations, the landslide hazard zonation, and the two-dimensional limit equilibrium analysis is included in this chapter, as follows:

Susceptibility Parameter

In the previous research, in which this current probability model was applied and analyzed as a first trial (Rodriguez-Yepes, 2011), it had a notorious limitation, the lack of engineering properties that could cover all the area of study. Parameters like the friction angle, the intercept of cohesion, or the shear modulus, are difficult to get, even in developed countries. These parameters would create an ideal scenario to evaluate landslide hazard in terms of probability. Here, two fundamental reasons did not allow the accomplishment of this task. Firstly, the model was initially conceived for large areas like a country. Secondly, there is going to be an evident problem of scale when dealing with geomechanical and this probability model (SGC, Colombian Geological Survey, 2016). This second reason has a strong background if it is recognized that the probability model is associated to the application and zonation of landslide hazard in large areas, geological areas, and its consequent geological scale. Then, geomechanical properties “strength-deformations-permeability” are an engineering description which is obviously associated to geotechnical areas and its consequent geotechnical scale. A geotechnical engineering scale is fundamentally different to a geological scale. So, the probability methodology for landslide hazard zonation was applied to the two landslides in Pipiral, a Central small Region of Colombia, using the slope angle as the susceptibility parameter again. Here, the two landslides were divided in “2.0*2.0 m2” and the probability model was evaluated again. This second trial helped validate the model and have a better approach to the application of the methodology. Then, to try to cover the limitation of including geomechanical properties in this research project, and to make it possible to refer in more geotechnical engineering terms, two-dimensional limit equilibrium analysis and Finite Element Analysis were modeled. The friction angle and the modulus of elasticity were calculated via correlations with SPT (standard penetration test) results. This item will be explained in the following chapter, in a more thorough form [6-10].

Seismicity parameters

Three parameters will be used to calculate the probability of landslide occurrence due to earthquakes: susceptibility function, the probability of occurrence of the critical earthquakes, and the probability that this critical earthquake triggers landslides in a specific “2.0*2.0 m2” cell. In this subchapter, the information used to get these three parameters will be explained, and in the following chapter, the methodology and corresponding calculations will be explained in a more thorough way.

• Susceptibility function: the slope angle was used as the susceptibility function. A normal distribution formulation that better explains how slope angle influences stability of a slope, was applied.

• Probability of occurrence of the critical earthquake: here, the seismic hazard evaluation report for the area that covers the two landslides was used (SGC, Colombian Geological Survey), and the probability of occurrence of the critical earthquake was calculated using the “Gutenberg-Richter” relationship. Seven seismogenic sources were identified. Seven geological faults that are close enough to the areas of study to influence them. The scale and the size of the landslides were the main factors to choose these seven geological faults. The area of the landslides, as mentioned above, were divided in “2.0*2.0 m2” cells, and the geological faults were divided in “2.0 meters” spaces. Figure 1 shows an explanatory scheme of how distances from each cell in the two landslides to the 2-meter divisions of the geological faults were measured:

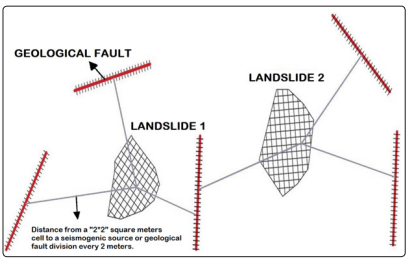
Figure 1: Explanatory Scheme of the measurement of the distance from the landslide?s cells and the divisions in the geological faults, to calculate the probability of occurrence of the critical earthquake (Yepes - Mosquera, 2019)

Figure 2 presents the geological faults, the location of the two landslides, the location of the specific region in Colombia and the names of the faults.

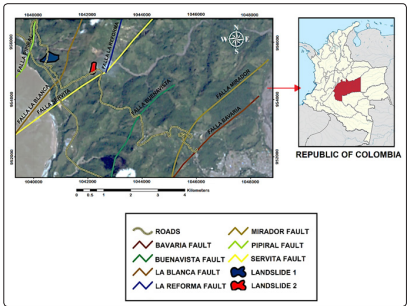
Figure 2: Geological faults from the seismic hazard study and location of the landslides (left). Location of “El Meta” Department in the map of Colombia (top right). Names of the faults and landslides (bottom right). (SGC, Colombian Geological Survey)

Probability that the critical earthquake triggers landslides: supported and calculated by a historical worldwide database of earthquake - induced landslides (Rodriguez and Yepes, 1767B.C. - 2007) updated by Mosquera (2007-2019).

Then, as it was initially proposed by the probability model, this updated database was classified in the three failure mechanisms proposed by Keefer (1984): disrupted landslides, coherent landslides, and lateral spread and flows. The total number of earthquake-induced landslides available in this updated database are: 472 disrupted landslide, 141 coherent landslides, and 134 lateral spread and flows. Keefer presented a database of earthquake induced landslides and a plot of Surface wave magnitude “Ms” versus Maximum epicentral distance, showing a 0% and 100% probability of slope failure due to landslides. Rodriguez and Yepes (2011), following the idea of Keefer, proposed now curves from 0% to 100% each approximately 10%. This was plotted for thethree failure mechanisms mentioned above. Mosquera and Yepes (2019) updated these plots, and figure 3 shows the landslide density curves or probability of failure for the latter mechanism: lateral spread and flows. There are two points below the 0% curve and one point above de 100% curve. They were defined as extraordinary and unusual behavior. They are out of the trend [16-20].

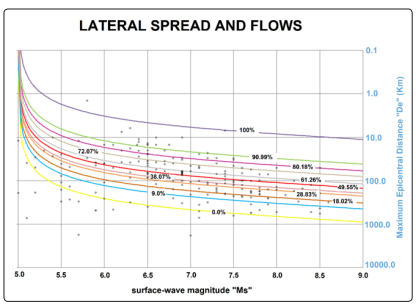
Figure 3: Landslide density curves or probability of landslide occurrence curves for Earthquake-Induced Landslides - Lateral Spread and Flows (Earthquake-Induced Landslides, 1767 B.C. - 2019) (Rodriguez - 2002, Yepes - 2009, Mosquera - 2019)

Rainfall parameters

The probability of landslide occurrence due to rainfall will be thoroughly explained in the next chapter. In this subchapter, and similar to how earthquake induced landslides are treated, to calculate the probability of landslide occurrence triggered by rainfall is composed by three parameters: a susceptibility function, the probability of occurrence of the critical rainfall, and the probability that the critical rainfall effectively generates landslides [21-30].

• Susceptibility function: the same function used for earthquake induced landslides was used in this case.

• Probability of occurrence of the critical rainfall: here, the “Intensity-duration-frequency” curves (IDF) that were closer to the critical landslides evaluated in this project, and in a proper scale, were used. Two rainfall stations were identified: La Esmeralda and Servita. Figure 4 shows IDF curves for the “Servita” rainfall Station for return periods of: 2, 5, 10, 25, 50, 75, 100, and 500 years.

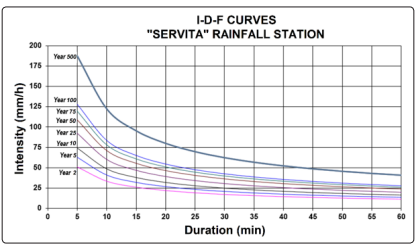
Figure 4: Intensity-Duration-Frequency curves for Servita Rainfall Station. Return periods of 2, 5, 10, 25, 50, 75, 100, and 500 years. (IDEAM, “Institute of Hydrology, Meteorology and Environmental studies” - Colombia)

• Probability that the critical rainfall triggers a landslide: supported and calculated by a historical database of rainfall - induced landslides in four countries of Central America where fine-grained soils are frequent in all their territory: El Salvador, Guatemala, Nicaragua, and Honduras (1982 - 2007, Yepes). This was updated by Mosquera (2007-2019), including historical rainfall-induced landslides in Colombia.

As it is possible to infer, the criteria for this database are different from the database for earthquake - induced landslides. In this case, the criteria were the type of soil, because the saturation of a slope and the generation of pore water pressure that triggers landslides works different in fine-grained soils, in coarse-grained soils, and in rocks. Landslide density curves or probability of occurrence curves were also defined for rainfall-induced landslides, in a similar form to earthquake-induced landslides, now plotting Intensity of the rain that caused the landslides versus the duration of this rain. Figure 5 shows this plot.

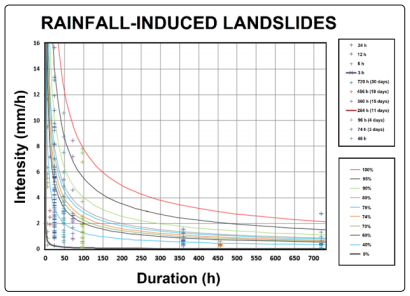
Figure 5: Landslide density curves or probability of landslide occurrence curves for Rainfall-Induced Landslides - (RainfallInduced Landslides, 1982 - 2019) (Yepes, Mosquera - 2019)

Geomechanical parameters from field investigation

As previously mentioned, the probability model was initially proposed for large areas of study, like a country. In this scenario, the use of geomechanical properties is not actually appropriate because of the scale. That is why, in this research project, zonation and modeling are treated and analyzed separately. In this subchapter, the use of strength and strain properties will be addressed: limit equilibrium to calculate factors of safety and finite element to study deformations of the two landslides.

Two-dimensional limit equilibrium and finite Element analysis:

using subsurface exploration performed in the two evaluated landslides and taking information close to surface to focus on local and surface failures, limit equilibrium and finite element analysis were performed. The results are presented in the next chapters.

Due to the difficulty to get samples like Shelby tubes to take to the lab and perform strength and deformability tests, SPT results are the only available information.

The friction angle was calculated for the identified layers from SPT results, using correlations that have been proved valid in Colombia (Gonzalez, 1999). Also, the modulus of elasticity was calculated from the same SPT results, using correlations from the accepted literature (Bowles, 2001)

The two analyzed landslides have had problems of stability for several years. Both this reason and the lack of alternatives of probabilistic and numerical methods to strictly try to find solutions to these types of problems, inspired this current project.

Analysis Method

The following information was taken from “Rodriguez and Yepes (2011)” and complemented throughout this paper. Landslide hazard was defined as failure probability considering rainfall, earthquake, and slope susceptibility effects. In this subchapter, the method used to obtain that probability is briefly explained.

Total probability

Total probability of failure of a given slope is obtained using Equation 1. Equation one is based on Bayes?s Theorem for mutually exclusive and independent events: earthquakes and rainfall.

P_t(F)=P(R)+P(S)-P(R)*P(S) (1)

“Pt (F)” is the total probability of failure, “P(R)” is the probability of failure due to rainfalls and “P(S)” is the probability of failure due to earthquakes.

“P(R)” is obtained using Equation 2, where “pr ” is the probability of occurrence of a given critical rainfall, “pfr” is the probability that the critical rainfall induces landslide in the slope, and “S” is a function that defines the slope susceptibility to Land sliding.

P(R)=p^r*p^fr*S (2)

“P(S)” is obtained using Equation 3, where “ps ” is the probability of exceedance of a given earthquake magnitude, “pfs” is the probability that the seismic events induce the slope failure, and “S” the slope susceptibility. In this paper “S” was consider the same for rainfall and earthquake-induced landslides.

P(S)=p^s*p^fs*S (3)

Equations (1), (2), and (3), are probability theory for two events that are independent and not mutually exclusive. Rainfall and earthquakes happen to be events with these two specific features.

Results

The probability model presented above and previously applied to El Salvador (Rodriguez-Yepes, 2011) was applied to the two problematic and constant landslides also mentioned before, and located in Pipiral, a small region in Central Colombia. The following figures show the results of zonation and two-dimensional analysis.

Landslide hazard Zonation

The following figures show: the probability of failure due to earthquakes, the probability of failure due to rainfall, and the total probability including both events as factors that can occur simultaneously, but with the condition that only one of them will cause the landslide for a given cell (2.0 * 2.0 m ² ).

Probability of failure due to earthquakes “P(S)”

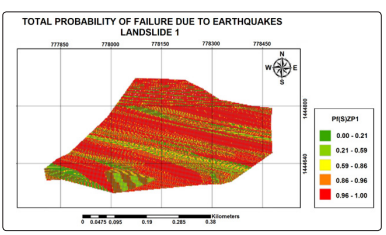
Figure 6: Probability of Failure due to earthquakes for Landslide 1 (Yepes - Mosquera, 2019)

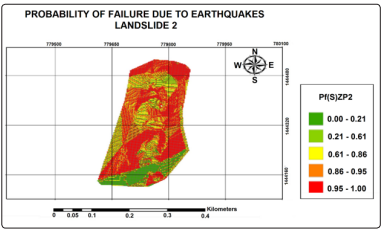
Figure 7: Probability of Failure due to earthquakes for Landslide 2 (Yepes - Mosquera, 2019)

Probability of failure due to rainfall “P(R)”

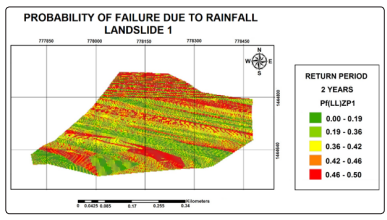
Figure 8: Probability of Failure due to Rainfall for Landslide 1 (Yepes - Mosquera, 2019)

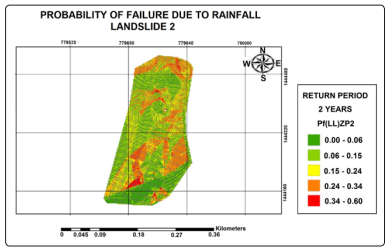
Figure 9: Probability of Failure due to Rainfall for Landslide 2 (Yepes - Mosquera, 2019)

Total Probability of failure “Pt (F)”

The following figure shows the probability of occurrence of the two events “rainfall and earthquakes”, with the condition that only one of them will trigger a landslide.

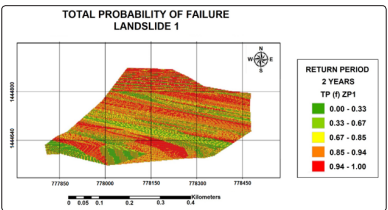
Figure 10: Total Probability of Failure for Landslide 1 (Yepes - Mosquera, 2019)

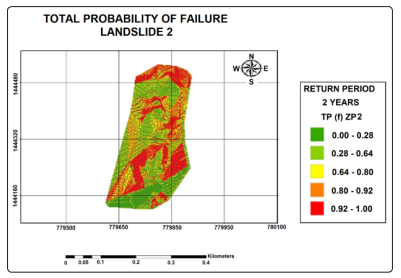
Figure 11: Total Probability of Failure for Landslide 2 (Yepes - Mosquera, 2019)

Two-dimensional analysis

Table 1 presents the geomechanical properties calculated using correlations with SPT results.

Table 1: Geomechanical properties for the layers found and defined with the subsurface exploration

GEMOECHANICAL PROPERTIES	STRENGTH		DEFORMABILITY
MATERIAL	Φu' (°)	Υ (KN/m3 )	E (kPa)	G (kPa)
Layer 1: residual soil, fine grained	27	18	4045	1667
Layer 2: colluvial soil	29	22	16502	6374
Layer 3: sedimentary rock	32	24	19613	7551
Layer 4: igneous rock	35	24	19613	7551

Using the friction angle as the strength property for the factor of safety, and the modulus of elasticity as the deformability property for the finite element analysis, the two-dimensional analysis was carried out. Figure 12 shows, for landslide 1:

• Top - left plan view of Landslide 1. Three sections, the most critical in red color
• Top - right: Factor of safety for the most critical section. The lowest factors of safety are close to surface.
• Bottom - left finite element analysis for the most critical section. Vectors showing the potential direction of the landslide. Surface stability problem is the most probable cause.
• Bottom right: location of subsurface exploration.

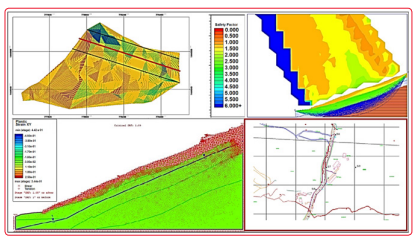
Figure 12: Two-dimensional evaluation. Limit equilibrium and Finite Element Analysis

For the Finite Element Analysis, as an analysis method that studies “Stress-strain” behavior before plastic behavior of the slope, each node of the two landslides has the geomechanical parameters included in table 1. The deformation vectors in red color shown in figure 12, present the portion of the slope that has a high potential of instability. The vectors clearly show that the slope is unstable close to surface, which is the current and actual geotechnical behavior of the area.

Figure 13 shows, for landslide 2, factors of safety of 0.748 close the surface, which indicates problems related with surface stability.

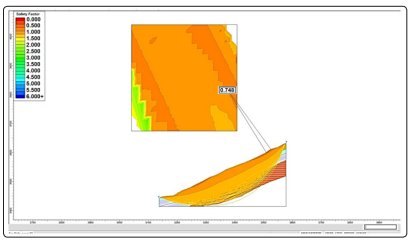
Figure 13: Two-dimensional evaluation. Factor of safety showing stability problems

For the Limit Equilibrium Analysis, as an analysis method that studies plastic behavior of the slope, the two landslides have the geomechanical parameters included in table 1. The factors of safety shown in figure 13, present the portion of the slope that has a high potential of instability. The factors of safety clearly show that the slope is unstable close to surface, which is the current and actual geotechnical behavior of the area [30-41].

Conclusions

• This application of the model shows it is a coherent approach to the current reality of the landslides and the reality of the past few years.
• The probability of occurrence of landslide due to earthquakes (eq. 3) included in the model (eq. 1), is linked to the seismic hazard analysis of the evaluated area. The methodology can be applied to a problematic area where the earthquakes are frequent triggers of landslides.
• The probability of occurrence of landslide due to rainfall (eq. 2) included in the model (eq. 3), is linked to I-D-F curves of the evaluated area. The methodology can be applied to a problematic area where rainfall is a frequent trigger of landslides.
• The probability model (eq.3) is ideal for regions where both rainfall and earthquakes are triggers of landslides. The summation of dynamic geological processes, frequent rainfall, variable topography, and complicated earth materials frequently generate landslides around the world.
• Both Finite Element and Limit Equilibrium analysis, although on a different scale than zonation, show and prove that the two evaluated areas are in a constant instability.
• It is fundamental to recognize the difference between the information used for zonation and for modeling. For landslide hazard zonation, the information is mainly “geologicalseismic-hydrological-topographic”. For two-dimensional modeling, the information is mainly “geotechnicalpseudostatic-topographic”.
• Even though, zonation and modeling come from different theoretical and scales scenarios, both show the instability that is currently occurring and has been occurring for several years in this specific evaluated area of Colombia.
• The urgent need to keep on using probability and numerical methods to evaluate hazard and to consequently evaluate risk, still requires many efforts, new research ideas, and valid applications from all the professionals involved in these types of studies. The use of more numerical methods instead of “qualitative, empirical” methods, increase the odds of having a better solution of a problem in civil engineering.
• The application of probability methodologies in geotechnical engineering, as one the numerical options available, is a genuine way to consider all the variables it is possible to find in nature.
• The probability of failure due to rainfall has values up to approximately 60%. This may be influenced by the fact that IDF information comes from only two rainfall stations that are close to the two studied landslides.
• The probability of failure due to earthquakes has values greater than 90%. This may be because the seismic hazard analysis has information from seven geological faults. Finally, the total probability of failure has values up to 90% and more. A conclusion here is that the problems of stability are mainly caused and influenced by the seismic behavior.

References

1. Ankit Sharma, Ujjwal Sur, et al (2020). “Probabilistic Landslide Hazard Assessment using Statistical Information Value (SIV) and GIS Techniques. A Case Study of Himachal Pradesh, India”. Wiley Online Library
2. Aneas S (2000) Risks and Dangers, a vision from geography. Retrieved from: http://www.ub.edu/geocrit/sn-60.htm.
3. Baroň I, Kycl P, Hradecký P, Metelka V, Vorel T, et al. (2007) Identifying the Areas Susceptible to Landsliding And Other Hazardous Processes In El Salvador, Nicaragua And Costa Rica, Central America. Proceedings of 1st North American Landslide Conference, Vail, Colorado.
4. Baecher G, Christian J (2003) Reliability and Statistics. Geotechnical Engineering.
5. Benito B, (2009) “Evaluación Regional de la Amenaza Sísmica en Centroamérica” - Proyect: RESIS II Final Report. Universidad Politécnica de Madrid, Madrid, Spain. 21p.
6. Burbach GV, Forhlich C, Pennington WD, Matumoto T (1984) Seismicity and tectonics of the subducted Cocos Plate. J. Geohys. Res., B. 89(B9): 7719-7735.
7. Colombian Association of Seismic Engineering [AIS]. Instituto Colombiano de Geología y Minería (1996). “Estudio general de amenaza sísmica de Colombia. Bogotá”.
8. Crone AJ, Baum RL, Lidke DJ, Sather DND, Bradley LA, et al. (2001) Landslides induced for Hurricane Mitch in El Salvador-An inventory and descriptions of selected features. Open-File Report 01-444. U.S. Geological Survey. Denver, Colorado 24p.
9. Christian John, Ladd Charles, Baecher G (1994) Reliability Applied to Slope Stability Analysis. Journal of Geotechnical Engineering 120: 2180-2207.
10. Chávez Agnes, González F (2018) “Caracterización mineralógica, porosimétrica, microestructural y con ensayos convencionales de agregados pétreos gruesos de una cantera del piedemonte llanero colombiano según norma IDU sección 500-11” (Universidad Católica de Colombia. Trabajo de postgrado. Bogotá). Retrieved from: https://repository. ucatolica.edu.co/bitstream/10983/16043/1/Trabajo de Grado_ final.pdf.
11. Cortés Ricardo, De la Espriella R (1990) Apuntes sobre la Tectónica del Valle del Río Negro al Oriente de Cundinamarca. Geología Colombiana 17: 133-142.
12. Dewey JW, Suárez G (1991) Seismotectonics of Middle America. In Neotectonics of North America, Slemmons et al. (eds), Geological Society of America, Decade Map 1: 309-321.
13. Ering, Sivakumar (2016) Probabilistic back analysis of rainfall induced landslide- A case study of Malin landslide. India, June: A case study of Malin landslide.
14. Escobar Carlos, Duque G (2017) “Análisis de estabilidad de taludes”. Retrieved from: https://cutt.ly/3wWPHxF.
15. Escobar H.E., Escobar M.R., Rendón J.R., (2003). “Caracterización geotécnica de las formaciones geológicas del área metropolitana de San Salvador y aplicación a la evaluación de amenaza por deslizamientos”. Civil Engineering Dissertation. Universidad Centroamericana “José Simeón Cañas”. San Salvador. El Salvador.
16. Estrategia Internacional para la Reducción de Desastres de las Naciones Unidas [UNISDR] (2009) “Terminología sobre reducción del riesgo de desastres” pp5-42. Retrieved from: www.preventionweb.net.
17. Garzón E (2016) “Propuesta metodológica para la evaluación de la amenaza de corredores viales de montaña de la red vial nacional”. In Actas de Ingeniería (Vol. 2). Retrieved from: http://fundacioniai.org/actas.
18. Gomis A (2007) “Localización de terremotos a partir de formas de onda”. Retrieved from: https://cutt.ly/cwWhf2X.
19. Gutenberg B, Richter C (1954) Seismicity of the Earth and Associated Phenomena.
20. Hadj-hamou T, Kavazanjian E (1985) Stability of Gentle Infinite Slopes. Journal of Geotechnical Engineering, ASCE 111: 681-697.
21. Harr M (1987) Reliability Based Design in Civil Engineering. In McGraw Hill.
22. Instituto Nacional de Investigaciones Geológico [INGEOMINAS] (1998) Memoria Explicativa Geología plancha 266 Villavicencio. Villavicencio, Meta: INGEOMINAS.
23. Instituto Nacional de Vías [INVIAS] (2013) Plancha 266 Villavicencio. Plano Geología Regional Sitios Críticos PR 82+410 a PR 93+500. Villavicencio, Meta.
24. Jiménez Gabriel, Viáfara J (2011) “Análisis 3D de drenes horizontales para la estabilización de taludes”. https:// repository.javeriana.edu.co/bitstream/handle/10554/7305/ tesis507.pdf?sequence=1&isAllowed=y.
25. Keefer DK (1984) Landslides caused by earthquakes. Geological Society of America Bulletin 95: 406-421.
26. Mesa Milena, Tejeda E (2018) “Análisis de la estabilidad de taludes en terraplenes mediante los métodos de equilibrio límite y el método de elementos finitos”. Revista Cubana de Ingenieria, IX 1: 49-56.
27. Mora S, Vahrson W (1994) Macrozonation Methodology for Landslide Hazard Determination. Bulletin of the Association of Engineering Geology 31: 49-58.
28. Paris, Gabriel; Romero, J. (1994). “Fallas activas en Colombia (Vol. 34)”. Retrieved from: https://www2.sgc. gov.co/Publicaciones/Cientificas/Seriadas/Documents/ BoletinVolumen34No2-3.pdf.
29. Rodríguez C, Torres A, Leon E (2004) Landslide Hazard in El Salvador. Procecedings of ECI Conference on Geohazards 1-10.
30. Rodríguez C (2003) Models for Earthquake and Rain Induced Landslide. Universidad Nacional De Colombia. Norwegian geotechnical Institute. Trabajo de postgrado. Bogotá.
31. Rodríguez M (2005) Tectónica de placas. In Biología marina y oceanografía: Geomorfología y tectónica de placas (p. 124). Retrieved from: https://cutt.ly/DwImx48.
32. Rodríguez CE (2001) Hazard assessment of earthquakeinduced landslides on natural slopes. PhD Thesis. Imperial College, University of London, London, UK.
33. Rodriguez CE (2007) Earthquake-induced Landslides in Central America. Central America Geology Resources Hazards. Bundschuh J, Alvarado GE (eds). Taylor and Francis London 1331p.
34. Rueda K, García H, Teheran K, Torrenegra W (1988) Sistema de fallas Guaicaramo. Servicio Geológico Colombiana. Retrieved from: https://cutt.ly/ZwImNVo.
35. Saro Lee and Biswajeet Pradhan (2006) “Probabilistic landslide hazards and risk mapping on Penang Island, Malaysia”. Journal of Earth System Science
36. Sen Cai Jing, Jim Yeh Tian, Yan E, Hong Hao Yong, Yang Huang Shao, et al. (2017) Uncertainty of rainfall-induced landslides considering spatial variability of parameters.
37. Strauch R, Istanbulluoglu E, Riedel J (2019) “A new approach to mapping landslide hazards: a probabilistic integration of empirical and physically based models in the North Cascades of Washington, USA”. Natural Hazards and Earth System Sciences
38. Sheng Fu, Lixia Chen, et al. (2020) “Landslide hazard probability and risk assessment at the community level: a case of western Hubei, China. Natural Hazards and Earth System Sciences.
39. Vega, Johnny, Hidalgo C (2014) “Estimación de la amenaza por deslizamientos detonados por sismo y lluvia”. Revista EIA 11: 103-117.
40. White RA, (1991) Tectonic implications of upper-crustal seismicity in Central America. Neotectonics of North America, Slemmons et al. (eds), Geological Society of America, Decade Map 1: 323-338.
41. Yepes JE, (2009) Implementacion De Un Modelo Estocástico Para Evaluar Amenaza De Deslizamientos. MSc Dissertation. Universidad Nacional de Colombia, Bogotá, Colombia.

View PDF

Our Pubmed Indexed Articles

---

---

---