Author(s): Sowmya Ramesh Kumar* and Samarth Ramesh Kedilaya
Multivariate Time Series Analysis (MTSA) plays a pivotal role in forecasting within diverse domains by addressing the complexities arising from interdependencies among multiple variables. This exploration delves into the fundamentals, methodologies, and applications of MTSA, elucidating its role in enhancing predictive capabilities. The key concepts in MTSA, including Vector Autoregression, Cointegration, Error Correction Models, and Granger Causality, form the foundation for understanding dynamic relationships among variables. The methodology section outlines the critical steps in MTSA, such as model specification, estimation, diagnostics, and forecasting. Additionally, the abstract explores the capabilities of Artificial Intelligence (AI) in time-series forecasting, emphasizing improved accuracy, long-term trend recognition, dynamic pattern recognition, and the handling of seasonality and anomalies. Specific AI models, such as Recurrent Neural Networks (RNNs) with Long Short-Term Memory (LSTM), Echo State Networks (ESNs), and Online Learning Algorithms, are discussed in detail, along with practical implementation examples. Furthermore, the abstract introduces the benefits and challenges associated with MTSA. The benefits include comprehensive insights, improved forecast accuracy, and real-world relevance, while challenges encompass data and model complexity, explicability, and the validity of assumptions. The discussion emphasizes the need for innovative approaches to explain the predictions of complex models and highlights ongoing research in developing explanability frameworks.
Forecasting is a critical component of decision-making in various domains, ranging from finance and economics to weather forecasting and supply chain management. While univariate time series analysis focuses on predicting a single variable over time, many real-world scenarios involve interdependencies among multiple variables. Multivariate Time Series Analysis (MTSA) emerges as a powerful tool for forecasting in such complex environments. In this exploration, we delve into the principles, methodologies, and applications of MTSA, elucidating how it enhances predictive capabilities in the face of intricate interactions among multiple variables.
Multivariate Time Series Analysis Fundamentals Multivariate Time Series Analysis involves the simultaneous consideration of multiple time-dependent variables. Unlike univariate time series, where forecasting revolves around a single variable, MTSA accommodates dynamic relationships and dependencies among several variables evolving over time. The primary goal is to capture the joint behavior of these variables and leverage this knowledge for accurate and comprehensive forecasting.
VAR models are fundamental in MTSA, representing a system of equations where each variable is regressed on its lagged values and the lagged values of all other variables. VAR models capture the dynamic interactions among multiple variables and provide a framework for forecasting.
Cointegration is a crucial concept in MTSA, signifying a long- term equilibrium relationship among variables. Identifying cointegration helps in understanding the underlying economic or structural relationships and ensures more reliable forecasts.
ECM models are extensions of VAR models, incorporating the notion of cointegration. These models capture short-term deviations from long-term equilibrium and are particularly useful when analyzing non-stationary multivariate time series data.
Granger causality tests are employed to determine whether past values of one variable can predict future values of another. Understanding Granger causality is essential for uncovering directional relationships among variables in a multivariate time series.

Figure 1: Key Concepts in Multivariate Time-Series Analysis (MTSA)
Defining the appropriate model structure is foundational in MTSA. Researchers must identify the lag order, select relevant variables, and consider potential exogenous factors that might influence the system.
Estimating the parameters of the selected model involves using historical data to determine the relationships among variables. Techniques like maximum likelihood estimation or Bayesian methods are commonly employed in MTSA.
Diagnostic tests assess the validity of assumptions, including stationarity, normality, and the absence of autocorrelation in the model residuals. Rigorous diagnostics are crucial for ensuring the reliability of the model.
Once the model is validated, it can be used for forecasting future values of the variables. Forecast accuracy is continuously assessed, and the model may be refined or updated as new data becomes available.

Figure 2: Process of Non-Stationary Time-Series Forecasting [1]
The adaptability and continuous learning nature of AI contribute to improved forecasting accuracy. Artificial Intelligence (AI) in time-series space is a combination of Machine Learning and Deep Learning models. By understanding evolving patterns and adapting to changing conditions, the model can make more precise predictions, even in dynamic environments.
AI excels in recognizing and capturing long-term trends present in time-series data. This is particularly beneficial for forecasting scenarios where understanding the overarching patterns is crucial for making accurate predictions.
Time-series data often exhibits dynamic patterns that may change over different time periods. Generational AI's ability to recognize and adapt to these dynamic patterns ensures that the model remains effective in capturing evolving temporal relationships.
Many time-series datasets contain seasonal variations and anomalies. Generational AI, with its contextual understanding, is well-equipped to handle such complexities, ensuring robust forecasting performance even in the presence of irregularities.
Unlike some traditional time-series models that may be sensitive to initialization conditions, Generational AI's continuous learning mitigates the impact of initial conditions. This resilience contributes to more stable and reliable forecasting outcomes.
AI models for time-series forecasting encompass a variety of techniques that leverage continuous learning, adaptability, and contextual understanding across successive generations of data. Below are some prominent types of AI (deep learning and machine learning) models that can be applied to time-series forecasting:
RNNs, especially those enhanced with LSTM units, are well-suited for time-series forecasting due to their ability to capture long- term dependencies. Generational adaptation in RNNs involves continuous learning from new data, allowing the model to adapt to evolving patterns and trends over time.
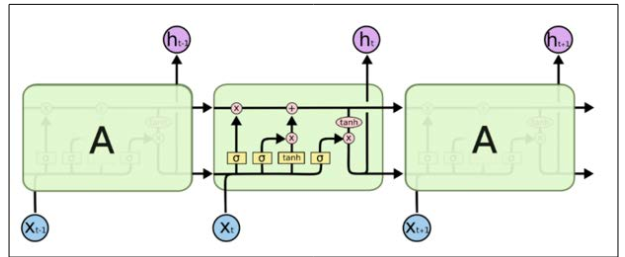
Figure 3: Internal Structure of LSTM [2]
Below is a code snippet to implement LSTM algorithm, Keras library along with Theano should be installed on a cluster of high performance computing center [2].


ESNs are a type of recurrent neural network designed for time- series analysis [3]. They consist of a fixed, randomly generated reservoir of neurons, and training involves adjusting only the output layer. ESNs can be adapted to new data, making them suitable for generational learning in time-series forecasting.
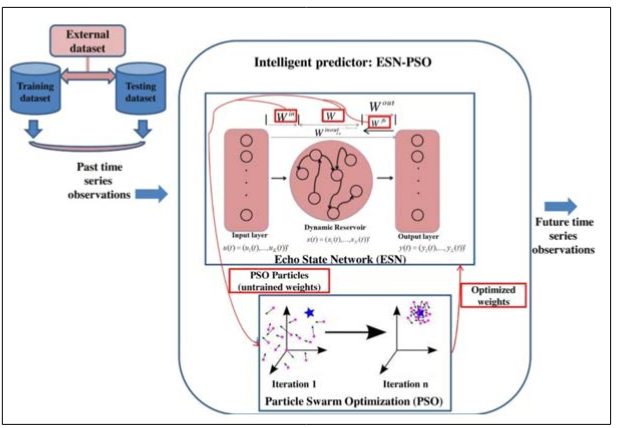
Figure 4: A Diagram of a Echo State Networks (ESNs) for Forecasting [3]
Algorithms designed for online learning, where the model is updated continuously as new data arrives, are inherently generational. Examples include online linear regression, online support vector machines, and online decision trees. These algorithms can be adapted to time-series forecasting scenarios for continuous learning.
Traditional machine learning models like linear regression, decision trees, or support vector machines can be adapted to generational learning by implementing incremental or online training. This involves updating the model parameters with new data, allowing it to learn continuously over time.
Ensemble models, such as Random Forests or Gradient Boosted Trees, can be designed with a continual or incremental learning approach. By updating the ensemble with new data and potentially introducing new base models, these models adapt to evolving patterns, making them suitable for generational time-series forecasting.
Specialized models like DeepAR, designed for probabilistic time-series forecasting using deep learning, can be adapted for generational learning. These models excel in capturing uncertainty and evolving patterns in time-series data.
Classic time-series forecasting models like ETS, which include components for error, trend, and seasonality, can be adapted to generational learning by updating the model parameters with each new generation of data. This allows them to continually adapt to changing patterns in the time series.
Hybrid models that combine traditional statistical methods with Bayesian techniques can offer generational learning capabilities. Bayesian methods inherently accommodate the integration of new information, making them suitable for adapting to evolving patterns in time-series data.
AutoML (Automated Machine Learning) platforms that incorporate automated feature engineering and model selection can adapt to new data automatically. These platforms continuously update models based on the latest data, providing generational learning capabilities for time-series forecasting.
Kalman Filters, commonly used for state estimation in dynamic systems, can be adapted for generational learning in time-series forecasting. By adjusting the filter parameters with each new data point, the model continuously adapts to changing dynamics.
In conclusion, this exploration provides a comprehensive overview of MTSA, incorporating AI methodologies, and underscores its significance in addressing the intricacies of forecasting in real- world scenarios. The synthesis of traditional models and AI techniques, along with continual adaptation through generational learning, offers a promising avenue for robust and accurate time- series forecasting.
Multivariate Time Series Analysis stands as a robust and indispensable tool in the data scientist's arsenal, particularly when forecasting involves the interplay of multiple variables. From economics and finance to supply chain management and public health, MTSA provides a framework for capturing the intricate relationships among variables, leading to more accurate and insightful predictions. As the complexities of real-world systems continue to evolve, the application of MTSA will likely expand, offering a potent approach to forecasting in an increasingly interconnected and dynamic world [5-9].
