Author(s): James McKelvie
Lorentz introduced his transformations as mere proposals for the relations between the E and H fields of light as measured in two reference systems in relative motion [1]. He proffered no argument to justify them. Others have subsequently given their own arguments to derive them, particularly in the context of Special Relativity. Seven derivations of the Lorentz transformations (LT's) are examined in detail. It is seen that all of them are invalid. The Appendix discusses the matter of equations and transformations. It is seen that a transformation is of necessity an inequality.
In his 1905 paper [2], Einstein derived the Lorentz Transformations, which derivation was fundamental to his discussion that followed. Actually, this was the first derivation. Lorentz introduced them merely as proposals.
Einstein’s 1905 paper (translated), is available free to download at http://hermes.ffn.ub.es/luisnavarro/nuevo_maletin/Einstein_1905_relativity.pdf
If there are mistakes in the derivation, what would that imply? (One would presume that it would be serious.) In fact, there two serious mistakes:
Einstein considers two Cartesian systems: K(x,y,z,t) which is stationary, and k(ξ,η,ζ,τ) which is moving in the positive x direction at υ with the x- ξ axes parallel. He introduces a parameter x′ = x – υt and [to quote] “it is clear that a point at rest in system k must have a set of values x′,y,z independent of time.", [present author’s italics because of the significance.]
Using what is a simple thought experiment (a light signal is sent and reflected back) he develops a differential equation: [to quote, - “applying the principle of the constancy of the velocity of light in the stationary system” – which implies “as viewed from within K”]. The equation in question is
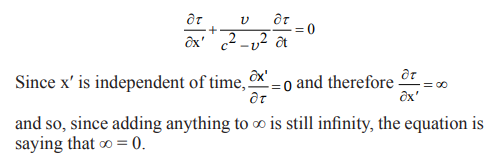













Using equation {6} is an essential step in his further argument leading to the LT′s, and so we can have no faith in this second derivation by Einstein.
Eddington [7] gives a derivation of the LT′s. However, at one point he says without any justification “Make the following transformation of coordinates...” So, mathematically, that is not a valid derivation. [He makes that transformation simply from having knowledge of Einstein’s result.]
Seven derivations of the LT′s have been examined and all have been shown to be invalid. However, that does not mean necessarily that Lorentz′s proposals for determining the relations for the E and H fields of light in moving reference frames are invalid. This is discussed in the Appendix. Further, it is obviously possible that some other worker may have presented a derivation which is not flawed, - but that seems to be unlikely, given the now general acceptance of the LT′s, there being no motivation to present yet another derivation.
Data Accessibility: This paper has no data
Ethics Statement: No work was done using human or animal items or tissues
Competing Interests: The author confirms that there are no competing interests associated with this article.
Author’s Contributions: There is only one author
Funding: The author confirms that there has been no source of funding for this work.
Appendix
The derivations of the Lorentz transformations have been shown to be invalid in the context of SR, but that does not mean that they may not be applied for the purpose for which they were originally proposed by Lorentz.
In Lorentz [1], a major purpose for the introduction of his transformations was for defining the Maxwell equations for light in a reference system moving at constant speed relative to the source. That is, to determine how the E and H fields change. He did not develop them by mathematical derivation. He simply “proposed” them. For instance, he says at his equation {3} “We shall further transform these formulae [present author’s italics] by a change of variables
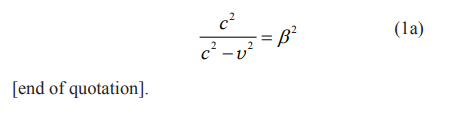
That was merely a proposal, with no preceding argument specifically for it. It is a relation to be used to develop a “transformation”. He does proceed thereafter with mathematical derivation using that proposal, but that means that his eventual conclusions are actually not truly totally derived. They are, at their heart, proposals.
It is a matter of regret that, in considering transformations, mathematicians have always used the equality sign “=”. If we consider a transformation that moves the line y = x by two units in the negative x-direction, it is given by x = x + 2. There is no such equality. It is an equation that that does not have any physical meaning. In mathematics and physics, it represents an impossibility.
But it is an effective transformation. What are we to make of that? The answer is that such a transformation represents, not an equality, but a replacement process. We replace x by x + 2. Strictly speaking we should have a symbol that means “is to be replaced by” – but such a symbol is not available to us.
So, whereas it has been shown above that Einstein’s (and others’) derivation of the transformations, - using only mathematics and ending up with an “equals” sign – is flawed, that does not mean that they are flawed as transformations, as Lorentz intended. As transformations are not equalities, we cannot make the kind of subsequent mathematical deductions that we are used to with equalities. In fact, a transformation is of necessity an inequality, for if it be an equality, then we are replacing the variable by something that is actually the same thing in a different guise, and there can be no resulting transformation.
There is nothing wrong with the following “transformation” which Lorentz might just as readily have written
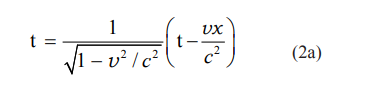
which is equation (1) with φ(υ) = 1 and the τ replaced by t, – just as there is nothing wrong with the transformation x = x + 2. The t’s are the same, and the equation looks to be impossible, but it is a perfectly valid transformation. It will give results for the E and H fields. (Of course, using that transformation (2a), nothing of SR would follow.)
Thus, Lorentz’s statement that “the variable t’ [his nomenclature] may be called ‘local time’” is not necessary. He could have dispensed with t’, by writing just t, and while having a “nonsense” equation, it would still be a valid transformation.
So, whereas the derivations of the LT’s considered here have been shown to be invalid, that does not mean that they are not valid for application to the Maxwell equations, because a transformation (2a), suffices, albeit it makes no sense as an equation.
It is a pity that there does not appear to be any experimental work having been done to investigate whether the proposals according to Lorentz for the E and H fields in a moving reference frame might be verified. But it is entirely possible that they are correct – though the LTs, as derived, expressed as equations and utilised in SR, are not valid - as derived in the seven examples quoted. [Of course, it is possible that a derivation that shows them to be valid may have been given and not come to the attention of the present author. But if they were shown to be equalities, then that would make them invalid as transformations, because to achieve a transformation the relation must, of necessity, be an inequality].
