Author(s): D. and S. Birks
In math circles, there are two ways of looking at π:
The number π is defined as the ratio of the length of a circle’s circumference to the length of its diameter, C/d (a mathematical constant approximately equal to 3.14).
But π is also defined in terms of degrees of a circle: specifically,

Of course, there’s only one problem with this equation: Where the circumference of a circle has degrees, the diameter and the radius do not. So here we have the commission of the ultimate mathematical transgression––the sin of mixing unities. In other words, by attempting to divide degrees by a length (mixing unities), this equation (showing π equal to 180 degrees) proves itself to be mathematically invalid.
Looking at this from a numerical angle, as the circumference will always be approximately 3.14 times the length of the diameter:
With this logic, as half the circle is also 180°, the conclusion is that π equals 180°.
Yes, there is no apparent division of degrees by length here, but on the other hand:
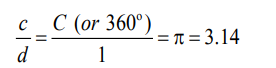
And applying the same logic, the conclusion would be that π is equal to 360°.
The problem is evident. How can this be?
Obviously, half the length of the circumference can never equal the full length. So, the question remains: How can 180° of half the circumference, and 360° of the circumference, both be equal to the same value of pi, 3.14 ?
Hmm, is it high time for science to do a 180? Anyway, to understand the mathematical mechanism at work here, think of the lengths of the circumference and diameter of a circle as corresponding to the base and height of a right triangle:
And so on and so forth. By calling an eighth of the diameter 1 (unity), then one-eighth of the circumference (and therefore, 45° of the circle) is equal to pi, 3.14. This can go on to infinity and beyond.
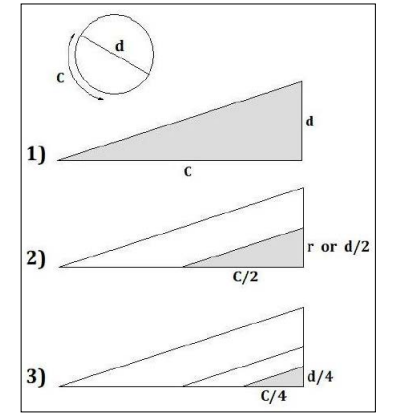
The process reveals the obvious: Changing the length of unity (what is called 1) just creates different-sized similar right triangles, whose heights and bases will always maintain their relative proportions to a circle and, thus, always maintain the numerical proportion of pi, 3.14. So the simple and unavoidable truth: By changing the length of unity, any portion of a circumference of a circle––and thus any angular degree (360°, 180°, 90°, 45°, etc.)––can be made to equal pi, 3.14 !
But now to sum up the thesis of this article, a final proof as to why C/d and pi can never equal 180°. (Yes, now for the coup de grâce, the final dagger in the heart of the lie of pi.) If you look at this next right triangle, in this configuration:
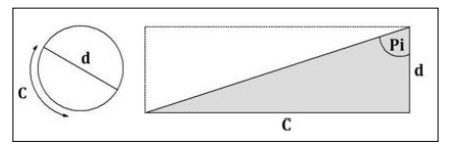
The ratio of the circumference of a circle divided by its diameter, C/d, is approximately 3.14. So with the circumference always three times greater than the diameter, logically you could never divide the actual length of the circumference by the length of the diameter and get half the length of the circumference. It’s a geometric impossibility.
Thus, as π and C/d can never equal half the circumference, or 180°, it is invalid to use π to represent 180° in any mathematics (in trigonometry, sine wave cycles and frequencies, quantum physics, etc.).
So where to from here?
Truth. Though it may be inconvenient to rewrite all those textbooks and manuals, to establish truth, 180° should be represented by some other symbol than π. To do otherwise would be academic dishonesty.
So, a rose by any other name? Which symbol to use––from alpha to omega––matters not, as long as half the circumference and 180° are never said to equal C/d and π.
But here is the real question: Who will be the true “pi-oneers” of the future? Who will be the first in the arena of physics and optics sciences with the courage to admit the truth, buck the establishment, academia, disrupt the status quo, and affirm that C/d and π can never equal or represent 180°?
View PDF